“珍珠编程”中的等式 - 有人可以解释一下吗？

Question

感觉我被卡住了，我的朋友们。有人可以解释我从“功能算法设计珍珠”第11章（“不是最大段总和”）中挑选方程式。

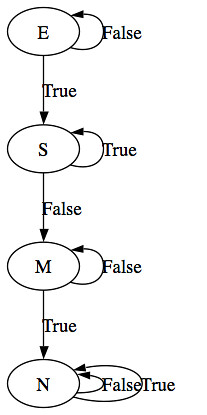
这是问题（稍微简化一点） 让我们给出一些给定转换的状态：

data State = E | S | M | N 
                deriving (Show, Eq) 

step E False = E 
step E True = S 
step S False = M 
step S True = S 
step M False = M 
step M True = N 
step N False = N 
step N True = N 

现在，我们来定义选择：

 pick q = map snd . filter ((== q) . fst) . map (\a -> (foldl step E a, a))

作者声称以下七个等式成立：

pick E xs = [[]]
pick S [ ] = [ ]
pick S (xs ++ [x]) = map (++[x ]) (pick S xs ++ pick E xs)
pick M [ ] = [ ]
pick M (xs ++ [x ]) = pick M xs ++ pick S xs
pick N [ ] = [ ]
pick N (xs ++ [x]) = pick N xs ++ map (++[x]) (pick N xs ++ pick M xs)

有人可以用简单的语言解释我，为什么这些方程式是真的，我们怎样才能证明一个明显的证明？我觉得我几乎理解S-方程式，但总的来说这仍然是难以捉摸的。

Answer 1

好的，我需要想象您的状态图：

并为pick :: State -> [[Bool]] -> [(State, [Bool])提供类型签名。

现在，这与你的第一个等式pick E xs = [[]]没有关系 - 它必须是pick E xs = [(E,[])]。

也许您打算以这种方式定义pick：

pick :: State -> [[Bool]] -> [[Bool]]
pick q = map snd . filter ((== q) . fst) . map (\a -> (foldl step E a, a))

假设这个定义，第一个等式现在有意义。它声称，如果您从E开始，xs中唯一以E结尾的布尔值序列就是空列表。

请注意，这假定[]∈xs。

此外，如果ys = replicate n False，pick E [ys] = [ys]，则这意味着∀n，ys∉xs。

第二，第四和第六个等式都是pick _ [ ] = [ ]的形式，map和filter的定义很简单。

第三个等式pick S (xs ++ [x]) = map (++[x ]) (pick S xs ++ pick E xs)也没有意义。我猜它试图说的是：

pick S (map (++[True] xs) = map (++[True]) (pick S xs ++ pick E xs)

也就是说 - 任何从E开始到S结尾的路径都可以通过将现有路径转到E或S并追加{{1}来构建}}。同样，每个以True结尾的路径都必须以S结尾。

第五个等式同样是荒谬的，应该表述为：

True

第七个等式应重述为：

pick S (map (++[False] xs) = map (++[False]) (pick S xs ++ pick M xs)