Question

对于bipartite graph，您可以将adjacency matrix替换为所谓的biadjacency matrix：

二部图的邻接矩阵A，其部分具有r和s顶点，形式为

    A =  O  B
         B^T O

其中B是r×s矩阵，O是全零矩阵。显然，矩阵B唯一地表示二分图，它通常被称为它的双边矩阵。

现在，DAG是一个二分图，例如，你可以topologically sort它，并且U和V集合分别是奇数或偶数拓扑级别的节点。

这意味着，对于具有n个节点的DAG，我只需要（n / 2）²矩阵（平均而言）而不是n ²矩阵。问题是，我不知道如何构建它。任何提示？

Answer 1

我相信你不能为DAG构建一个biadjacency矩阵，因为不是每个DAG都是一个二分图。

这是一个简单的例子：考虑一个有3个顶点的有向图，并将它们表示为A，B和C.边缘连接A到B，B到C和A到C.图形显然是DAG，因为它被引导并且没有循环（A-> B-> C＆lt; -A不是循环）。但是，图形不是二分图：没有办法将A，B和C分成两个不相交的集合，其中同一集合中的顶点之间没有边缘。

结论是有图表是DAG而不是二分图，因此不是每个DAG都是二分图。

请注意，您可以在拓扑上对DAG进行排序并将顶点划分为两个不相交的集合，这并不意味着同一集合的顶点之间没有边缘。

Answer 2

似乎A矩阵的biadjacency矩阵B只能在图表无方向时构建。

基于维基百科的例子：

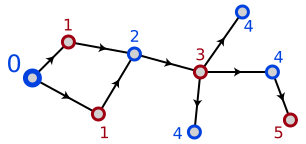
此DAG的邻接矩阵应为：

Blue -> Red
B = 1 1 0 0
    0 0 1 0
    0 0 0 0
    0 0 0 0
    0 0 0 1

Red -> Blue
C = 0 1 0 0 0
    0 1 0 0 0
    0 0 1 1 1
    0 0 0 0 0

正如您所看到的，C不是B的转置。似乎无法创建所描述的A矩阵。但是，您可以创建一个这样的A矩阵：

A = 0 B
    C 0

这将需要2 *（n / 2）^ 2空间，这仍然优于n ^ 2.

要构建B和C矩阵，您只需要在U和V（分别）中遍历每个节点以确定出站边缘。

Answer 3

以下代码将创建给定邻接矩阵的biadjacency矩阵，如果它是bipatite（只有bipatite图形具有biadjacency矩阵。）如果给定的图形不是bipatite，则GetBiadjacencyMatrix（）方法返回null。

Graph of the provided sample including its biadjacency matrix http://www.freeimagehosting.net/image.php?10e9b6a746.jpg

看不到图像？ Click here

public class Matrix
{
    private void Usage()
    {
        int[,] AdjacencyMatrix = new int[,] { 
                                        {0, 1, 1, 0, 0, 0, 0, 0, 0},
                                        {1, 0, 0, 1, 0, 0, 0, 0, 0},
                                        {1, 0, 0, 1, 0, 0, 0, 0, 0},
                                        {0, 1, 1, 0, 1, 0, 0, 0, 0},
                                        {0, 0, 0, 1, 0, 1, 1, 1, 0},
                                        {0, 0, 0, 0, 1, 0, 0, 0, 0},
                                        {0, 0, 0, 0, 1, 0, 0, 0, 0},
                                        {0, 0, 0, 0, 1, 0, 0, 0, 1},
                                        {0, 0, 0, 0, 0, 0, 0, 1, 0}
                                       };

        int[,] BiadjacencyMatrix = GetBiadjacencyMatrix(AdjacencyMatrix);
    }

    public static int[,] GetBiadjacencyMatrix(int[,] adjacencyMatrix)
    {
        int NodeCount = adjacencyMatrix.GetLength(0);

        NodeInfo[] Nodes = new NodeInfo[NodeCount];
        for (int c = NodeCount - 1; c >= 0; c--)
            Nodes[c] = new NodeInfo(c);

        if (ColorNode(adjacencyMatrix, Nodes, 0, 1, -1) != NodeCount)
            return null; // Given graph is not bipatite.

        int Part1Count = 0, Part2Count = 0;
        foreach (NodeInfo Node in Nodes)
            Node.IndexInPart = Node.PartID == 1 ? Part1Count++ : Part2Count++;

        int[,] ToReturn = new int[Part1Count, Part2Count];
        foreach (NodeInfo NodeInPart1 in Nodes)
            if (NodeInPart1.PartID == 1)
                foreach (NodeInfo NodeInPart2 in Nodes)
                    if (NodeInPart2.PartID == 2)
                        ToReturn[NodeInPart1.IndexInPart, NodeInPart2.IndexInPart]
                            = adjacencyMatrix[NodeInPart1.IndexInGraph, NodeInPart2.IndexInGraph];

        return ToReturn;
    }

    private static int ColorNode(int[,] adjacencyMatrix, NodeInfo[] nodes, int currentNode, int currentPart, int parentNode)
    {
        if (nodes[currentNode].PartID != -1) 
            return nodes[currentNode].PartID != currentPart ? -1 : 0;
        int ToReturn = 1;
        nodes[currentNode].PartID = currentPart;
        for (int c = nodes.Length - 1; c >= 0; c--)
            if (adjacencyMatrix[currentNode, c] != 0 && c != parentNode)
            {
                int More = ColorNode(adjacencyMatrix, nodes, c, currentPart == 1 ? 2 : 1, currentNode);
                if (More == -1) return -1;
                ToReturn += More;
            }
        return ToReturn;
    }
}


public class NodeInfo
{
    private int _IndexInGraph;
    private int _PartID;
    private int _IndexInPart;
    private bool _IsVisited;

    public NodeInfo(int indexInGraph)
    {
        _IndexInGraph = indexInGraph;
        _PartID = -1;
        _IndexInPart = -1;
        _IsVisited = false;
    }

    public int IndexInGraph
    {
        get { return _IndexInGraph; }
        set { _IndexInGraph = value; }
    }

    public int PartID
    {
        get { return _PartID; }
        set { _PartID = value; }
    }

    public int IndexInPart
    {
        get { return _IndexInPart; }
        set { _IndexInPart = value; }
    }

    public bool IsVisited
    {
        get { return _IsVisited; }
        set { _IsVisited = value; }
    }
}

Answer 4

你所说的biadjacency矩阵的对称性，和你打算使用拓扑排序来分离图中的二分结构 - 指出你实际上指的是间接的，非循环，图形 - 即树。（对称明确表示，如果你有一条从x到y的边，你必须有一条从y到x的边 - 因此，定向变得毫无意义。）

假设确实是你的意图：

（1）对于任何间接图，你可以立即稳定约0.5 *（n ^ 2）（确切地说：n（n-1）/ 2），只存储上层邻接矩阵的三角形。

（2）假设你必须只储存B.

你必须首先确定不相交的子集，比如说R＆amp; S，每个都没有内部边缘。拓扑排序是一个合理的选择 - 在树中，它相当于选择一个根并通过在根上方的偶数/奇数级别标记顶点（与common visualizations相比，我更喜欢将树视为实际增长上面它的根...）。我从你的问题中了解到你对此感到满意，所以我甚至不会给出伪代码。

接下来，您需要重新标记顶点，以便所有R的顶点先到，并且所有S的顶点都遵循：

Allocate NewLabels(r + s);
CurRSize = 0;
CurSSize = 0;
for each (TreeLevel)
    if #CurLevel is even  // append to R vertices
       NewLabels(CurRSize : CurRsize + CurLevelSize - 1) = CurLevelVertexNums;
       CurRSize += CurLevelSize;
    else // append to S vertices
       NewLabels(r+s - (CurSSize+CurLevelSize) : r+s - (CurSSize + 1) = CurLevelVertexNums;
       CurSSize += CurLevelSize;

（一些优化立即浮现在脑海中，但它们在这里并不重要。）

然后，您可以连续扫描图形边缘，并将它们作为条目存储到r x s矩阵B中，由 new 顶点标签索引：

Allocate B(r,s);
Zero(B);
for each (edge = x<-->y)
   i = NewLabels(x);
   j = NewLabels(y) - r; // must adjust, to index just B
   B(i,j) = 1;

HTH。

如何构建DAG的biadjacency矩阵？

4 个答案: