寻找齿轮齿的径向坐标描述
我不需要物理上准确的功能,但是需要提示渐开线曲线等等。我只是使用r = 2 + sin^2,它可以实现这个想法,但它看起来像是 - 咳咳。谷歌搜索,你可以找到关于如何起草“正确”装备的大量信息,但没有任何方法可以用于简单的近似。
编辑:我追求的“外观”:http://www.cartertools.com/involute.html
4 个答案:
答案 0 :(得分:2)
from pylab import *
nteeth = 30
inner = 10
outer = 12
# these are in teeth-hundredths, but half the actual measurement
bottom_width = 22
top_width = 15
def involute_r(angle):
'''angle is given in teeth-hundredths'''
angle = angle % 100
if angle > 50:
# symmetry
angle = 100 - angle
if angle < bottom_width:
return inner
if angle > (50 - top_width):
return outer
halfway = (inner + outer) / 2.0
transition_width = 50 - top_width - bottom_width
curve = 1.0 - (angle - (50 - top_width))**2 / (transition_width ** 2)
return halfway + curve * (outer - halfway)
fig = figure()
ax = fig.add_subplot(111, polar=True)
theta = np.arange(0, 2*pi, 0.001)
r = [involute_r(t * nteeth * 100 / (2 * pi)) for t in theta]
ax.plot(theta, r)
ax.set_ylim(inner, outer+1)
show()
答案 1 :(得分:0)
r = 2 + sin(24*theta)^12怎么样?如果你没有在问题中更具体,那就很难知道你想要什么。
答案 2 :(得分:0)
在我看来,好像关于involute curves的维基百科文章回答了你的问题。它说:
“在polar coordinates(r,θ)中,圆的渐开线具有参数方程:
r = a秒α
θ=tanα - α
其中a是圆的半径,α是参数。“
如果您需要以θ而不是α参数化的形式,那么您将需要以数字方式解决它,因为我认为没有符号解决方案。你还需要注意,因为在θ方面有无穷多的r解决方案(因为渐开线绕圆圈旋转的方式):
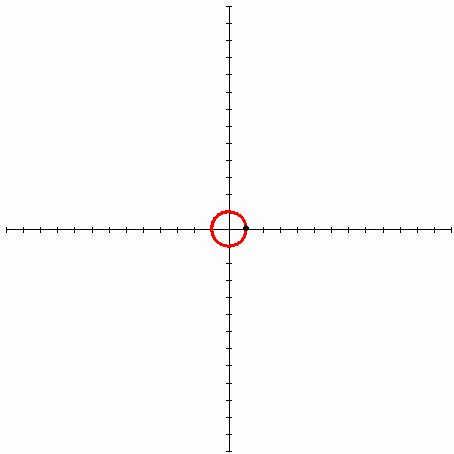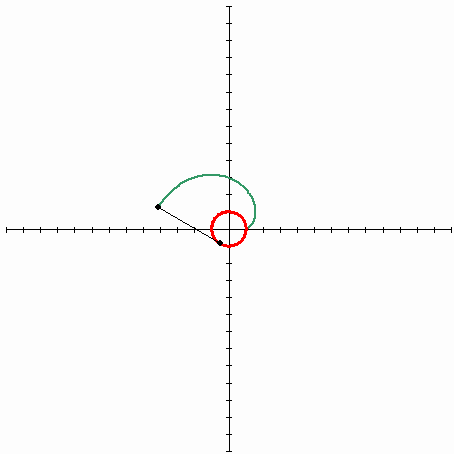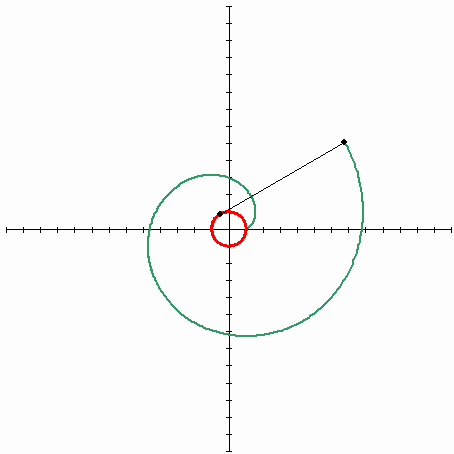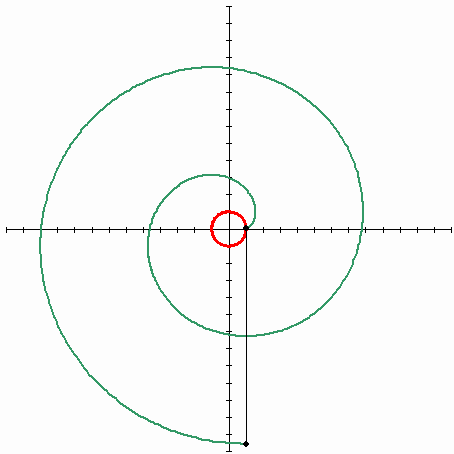
答案 3 :(得分:0)
渐开线的方程是正确的。您可以相对于音高半径使用它。我知道你不是准确的,但在实践中,这不是正确的形状。一本好的齿轮设计书将引导您完成所有关于诸如基部半径之类的古怪细节以减轻压力。你可以read old versions online using Google Books,这不是真正过时的东西。它真的非常迷人,你可能会在那里找到一些有助于使你的形状看起来真实的细节。
相关问题
最新问题
- 我写了这段代码,但我无法理解我的错误
- 我无法从一个代码实例的列表中删除 None 值,但我可以在另一个实例中。为什么它适用于一个细分市场而不适用于另一个细分市场?
- 是否有可能使 loadstring 不可能等于打印?卢阿
- java中的random.expovariate()
- Appscript 通过会议在 Google 日历中发送电子邮件和创建活动
- 为什么我的 Onclick 箭头功能在 React 中不起作用?
- 在此代码中是否有使用“this”的替代方法?
- 在 SQL Server 和 PostgreSQL 上查询,我如何从第一个表获得第二个表的可视化
- 每千个数字得到
- 更新了城市边界 KML 文件的来源?