如何计算文本中单词频率的最佳zipf分布

Question

对于家庭作业，我必须绘制文本的单词频率并将其与最佳zipf分布进行比较。

在对数对数图中根据文本的排名绘制计数的单词频率似乎很好。

但是我对计算最佳的zipf分布感到困惑。结果应如下所示：

我不明白计算zipf直线的方程式。

在zipf法的德国维基百科页面上，我发现了一个似乎有效的方程式

但是没有引用任何资料，所以我不知道1.78的常量来自哪里。

#tokenizes the file 
tokens = word_tokenize(raw)
tokensNLTK = Text(tokens)

#calculates the FreqDist of all words - all words in lower case
freq_list = FreqDist([w.lower() for w in tokensNLTK]).most_common()

#Data for X- and Y-Axis plot
values=[]
for item in (freq_list):
    value = (list(item)[1]) / len([w.lower() for w in tokensNLTK])
    values.append(value)

#graph of counted frequencies gets plotted
plt.yscale('log')
plt.xscale('log')
plt.plot(np.array(list(range(1, (len(values)+1)))), np.array(values))

#graph of optimal zipf distribution is plotted
optimal_zipf = 1/(np.array(list(range(1, (len(values)+1))))* np.log(1.78*len(values)))###1.78
plt.plot(np.array(list(range(1, (len(values)+1)))), optimal_zipf)
plt.show()

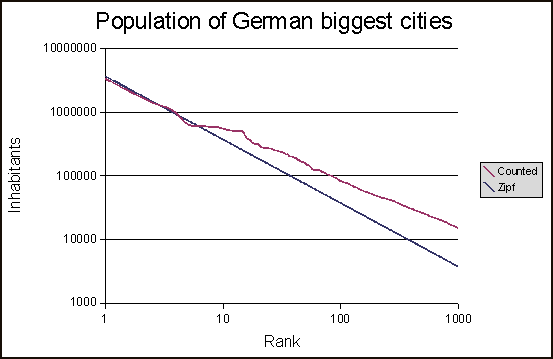
此脚本的结果如下：

但我只是不确定最优zipf分布是否计算正确。如果是这样，最优zipf分布是否不应该横穿X轴？

编辑：如果有帮助，我的文本有2440400个令牌和27491个类型

Answer 1

看看这个research paper by Andrew William Chisholm.具体的第22页。

  

H（N）≈ln（N）+γ

     

其中，γ是欧拉-马舍罗尼常数，近似值为0.57721。   注意exp（γ）≈1.78，方程式<...>可以重写为大N（N必须大于1,000才能精确到千分之一）。

     

pr≈1 / [r * ln（1.78 * N）]