Question

有没有办法在C中对齐指针？假设我正在将数据写入数组堆栈（因此指针向下移动）并且我希望我写入的下一个数据是4对齐的，因此数据写入的内存位置是4的倍数，我该怎么做是什么？

我有

 uint8_t ary[1024];
 ary = ary+1024;
 ary -= /* ... */

现在假设ary指向位置0x05。我希望它指向0x04。现在我可以做到

ary -= (ary % 4);

但是C不允许模指针。有没有与架构无关的解决方案？

Answer 1

数组是 NOT 指针，尽管你可能在这里读过误导的答案（特别是这个问题或者一般的Stack Overflow或其他任何地方）。

您无法更改数组名称所代表的值，如图所示。

可能令人困惑的是，如果ary是一个函数参数，那么看起来你可以调整数组：

void function(uint8_t ary[1024])
{
    ary += 213; // No problem because ary is a uint8_t pointer, not an array
    ...
}

作为函数参数的数组与函数外部或函数内部定义的数组不同。

你可以这样做：

uint8_t    ary[1024];
uint8_t   *stack = ary + 510;
uintptr_t  addr  = (uintptr_t)stack;

if (addr % 8 != 0)
    addr += 8 - addr % 8;
stack = (uint8_t *)addr;

这可确保stack中的值在8字节边界上对齐，向上舍入。您的问题要求舍入到4字节边界，因此代码更改为：

if (addr % 4 != 0)
    addr -= addr % 4;
stack = (uint8_t *)addr;

是的，您也可以使用位掩码。之一：

addr = (addr + (8 - 1)) & -8;  // Round up to 8-byte boundary

或：

addr &= -4;                    // Round down to a 4-byte boundary

只有当LHS是2的幂时才能正常工作 - 不是任意值。具有模数运算的代码将适用于任何（正）模数。

另请参阅： How to allocate aligned memory using only the standard library 。

演示代码

Gnzlbg commented：

如果我尝试对齐，例如两次断电的代码uintptr_t（2）最多1个字节的边界（两者都是2：2 ^ 1和2 ^ 0的幂）。结果为1但应为2，因为2已经与1字节边界对齐。

此代码演示了对齐代码是正常的 - 只要您正确解释上面的注释（现在通过'或者'分隔位屏蔽操作的单词澄清;我在第一次检查代码时被抓住了。）< / p>

对齐函数可以更紧凑地编写，特别是没有断言，但编译器将优化以从编写的内容和可编写的内容生成相同的代码。一些断言也可以更加严格。也许测试函数应该在执行任何其他操作之前打印出堆栈的基址。

代码可以，也许应该检查算术不会出现数字上溢或下溢。如果将地址与多兆字节边界对齐，这可能更有可能成为问题。当你保持在1 KiB，对齐之下时，如果你没有试图超出你可以访问的数组范围，你就不太可能发现问题。（严格地说，即使你进行多兆字节对齐，如果结果将在分配给你正在操作的数组的内存范围内，也不会遇到麻烦。）

#include <assert.h>
#include <stdint.h>
#include <stdio.h>

/*
** Because the test code works with pointers to functions, the inline
** function qualifier is moot.  In 'real' code using the functions, the
** inline might be useful.
*/

/* Align upwards - arithmetic mode (hence _a) */
static inline uint8_t *align_upwards_a(uint8_t *stack, uintptr_t align)
{
    assert(align > 0 && (align & (align - 1)) == 0); /* Power of 2 */
    assert(stack != 0);

    uintptr_t addr  = (uintptr_t)stack;
    if (addr % align != 0)
        addr += align - addr % align;
    assert(addr >= (uintptr_t)stack);
    return (uint8_t *)addr;
}

/* Align upwards - bit mask mode (hence _b) */
static inline uint8_t *align_upwards_b(uint8_t *stack, uintptr_t align)
{
    assert(align > 0 && (align & (align - 1)) == 0); /* Power of 2 */
    assert(stack != 0);

    uintptr_t addr  = (uintptr_t)stack;
    addr = (addr + (align - 1)) & -align;   // Round up to align-byte boundary
    assert(addr >= (uintptr_t)stack);
    return (uint8_t *)addr;
}

/* Align downwards - arithmetic mode (hence _a) */
static inline uint8_t *align_downwards_a(uint8_t *stack, uintptr_t align)
{
    assert(align > 0 && (align & (align - 1)) == 0); /* Power of 2 */
    assert(stack != 0);

    uintptr_t addr  = (uintptr_t)stack;
    addr -= addr % align;
    assert(addr <= (uintptr_t)stack);
    return (uint8_t *)addr;
}

/* Align downwards - bit mask mode (hence _b) */
static inline uint8_t *align_downwards_b(uint8_t *stack, uintptr_t align)
{
    assert(align > 0 && (align & (align - 1)) == 0); /* Power of 2 */
    assert(stack != 0);

    uintptr_t addr  = (uintptr_t)stack;
    addr &= -align;                         // Round down to align-byte boundary
    assert(addr <= (uintptr_t)stack);
    return (uint8_t *)addr;
}

static inline int inc_mod(int x, int n)
{
    assert(x >= 0 && x < n);
    if (++x >= n)
        x = 0;
    return x;
}

typedef uint8_t *(*Aligner)(uint8_t *addr, uintptr_t align);

static void test_aligners(const char *tag, Aligner align_a, Aligner align_b)
{
    const int align[] = { 64, 32, 16, 8, 4, 2, 1 };
    enum { NUM_ALIGN = sizeof(align) / sizeof(align[0]) };
    uint8_t stack[1024];
    uint8_t *sp = stack + sizeof(stack);
    int dec = 1;
    int a_idx = 0;

    printf("%s\n", tag);
    while (sp > stack)
    {
        sp -= dec++;
        uint8_t *sp_a = (*align_a)(sp, align[a_idx]);
        uint8_t *sp_b = (*align_b)(sp, align[a_idx]);
        printf("old %p, adj %.2d, A %p, B %p\n",
               (void *)sp, align[a_idx], (void *)sp_a, (void *)sp_b);
        assert(sp_a == sp_b);
        sp = sp_a;
        a_idx = inc_mod(a_idx, NUM_ALIGN);
    }
    putchar('\n');
}

int main(void)
{
    test_aligners("Align upwards", align_upwards_a, align_upwards_b);
    test_aligners("Align downwards", align_downwards_a, align_downwards_b);
    return 0;
}

示例输出（部分截断）：

Align upwards
old 0x7fff5ebcf4af, adj 64, A 0x7fff5ebcf4c0, B 0x7fff5ebcf4c0
old 0x7fff5ebcf4be, adj 32, A 0x7fff5ebcf4c0, B 0x7fff5ebcf4c0
old 0x7fff5ebcf4bd, adj 16, A 0x7fff5ebcf4c0, B 0x7fff5ebcf4c0
old 0x7fff5ebcf4bc, adj 08, A 0x7fff5ebcf4c0, B 0x7fff5ebcf4c0
old 0x7fff5ebcf4bb, adj 04, A 0x7fff5ebcf4bc, B 0x7fff5ebcf4bc
old 0x7fff5ebcf4b6, adj 02, A 0x7fff5ebcf4b6, B 0x7fff5ebcf4b6
old 0x7fff5ebcf4af, adj 01, A 0x7fff5ebcf4af, B 0x7fff5ebcf4af
old 0x7fff5ebcf4a7, adj 64, A 0x7fff5ebcf4c0, B 0x7fff5ebcf4c0
old 0x7fff5ebcf4b7, adj 32, A 0x7fff5ebcf4c0, B 0x7fff5ebcf4c0
old 0x7fff5ebcf4b6, adj 16, A 0x7fff5ebcf4c0, B 0x7fff5ebcf4c0
old 0x7fff5ebcf4b5, adj 08, A 0x7fff5ebcf4b8, B 0x7fff5ebcf4b8
old 0x7fff5ebcf4ac, adj 04, A 0x7fff5ebcf4ac, B 0x7fff5ebcf4ac
old 0x7fff5ebcf49f, adj 02, A 0x7fff5ebcf4a0, B 0x7fff5ebcf4a0
old 0x7fff5ebcf492, adj 01, A 0x7fff5ebcf492, B 0x7fff5ebcf492
…
old 0x7fff5ebcf0fb, adj 08, A 0x7fff5ebcf100, B 0x7fff5ebcf100
old 0x7fff5ebcf0ca, adj 04, A 0x7fff5ebcf0cc, B 0x7fff5ebcf0cc
old 0x7fff5ebcf095, adj 02, A 0x7fff5ebcf096, B 0x7fff5ebcf096

Align downwards
old 0x7fff5ebcf4af, adj 64, A 0x7fff5ebcf480, B 0x7fff5ebcf480
old 0x7fff5ebcf47e, adj 32, A 0x7fff5ebcf460, B 0x7fff5ebcf460
old 0x7fff5ebcf45d, adj 16, A 0x7fff5ebcf450, B 0x7fff5ebcf450
old 0x7fff5ebcf44c, adj 08, A 0x7fff5ebcf448, B 0x7fff5ebcf448
old 0x7fff5ebcf443, adj 04, A 0x7fff5ebcf440, B 0x7fff5ebcf440
old 0x7fff5ebcf43a, adj 02, A 0x7fff5ebcf43a, B 0x7fff5ebcf43a
old 0x7fff5ebcf433, adj 01, A 0x7fff5ebcf433, B 0x7fff5ebcf433
old 0x7fff5ebcf42b, adj 64, A 0x7fff5ebcf400, B 0x7fff5ebcf400
old 0x7fff5ebcf3f7, adj 32, A 0x7fff5ebcf3e0, B 0x7fff5ebcf3e0
old 0x7fff5ebcf3d6, adj 16, A 0x7fff5ebcf3d0, B 0x7fff5ebcf3d0
old 0x7fff5ebcf3c5, adj 08, A 0x7fff5ebcf3c0, B 0x7fff5ebcf3c0
old 0x7fff5ebcf3b4, adj 04, A 0x7fff5ebcf3b4, B 0x7fff5ebcf3b4
old 0x7fff5ebcf3a7, adj 02, A 0x7fff5ebcf3a6, B 0x7fff5ebcf3a6
old 0x7fff5ebcf398, adj 01, A 0x7fff5ebcf398, B 0x7fff5ebcf398
…
old 0x7fff5ebcf0f7, adj 01, A 0x7fff5ebcf0f7, B 0x7fff5ebcf0f7
old 0x7fff5ebcf0d3, adj 64, A 0x7fff5ebcf0c0, B 0x7fff5ebcf0c0
old 0x7fff5ebcf09b, adj 32, A 0x7fff5ebcf080, B 0x7fff5ebcf080

Answer 2

不要使用MODULO !!!真的很慢！按下最快的方式来对齐指针是使用2的补码数学。您需要反转这些位，添加一个，并屏蔽掉2（对于32位）或3（对于64位）最低有效位。结果是一个偏移量，然后您将其添加到指针值以对齐它。适用于32位和64位数字。对于16位对齐，只需用0x1屏蔽指针并添加该值。算法在任何语言中的工作方式都相同，但正如您所看到的，嵌入式C ++在各种形式和形式上都优于C语言。

#include <cstdint>
/** Returns the number to add to align the given pointer to a 8, 16, 32, or 64-bit 
    boundary.
    @author Cale McCollough.
    @param  ptr The address to align.
    @return The offset to add to the ptr to align it. */
template<typename T>
inline uintptr_t MemoryAlignOffset (const void* ptr) {
    return ((~reinterpret_cast<uintptr_t> (ptr)) + 1) & (sizeof (T) - 1);
}

/** Word aligns the given byte pointer up in addresses.
    @author Cale McCollough.
    @param ptr Pointer to align.
    @return Next word aligned up pointer. */
template<typename T>
inline T* MemoryAlign (T* ptr) {
    uintptr_t offset = MemoryAlignOffset<uintptr_t> (ptr);
    char* aligned_ptr = reinterpret_cast<char*> (ptr) + offset;
    return reinterpret_cast<T*> (aligned_ptr);
}

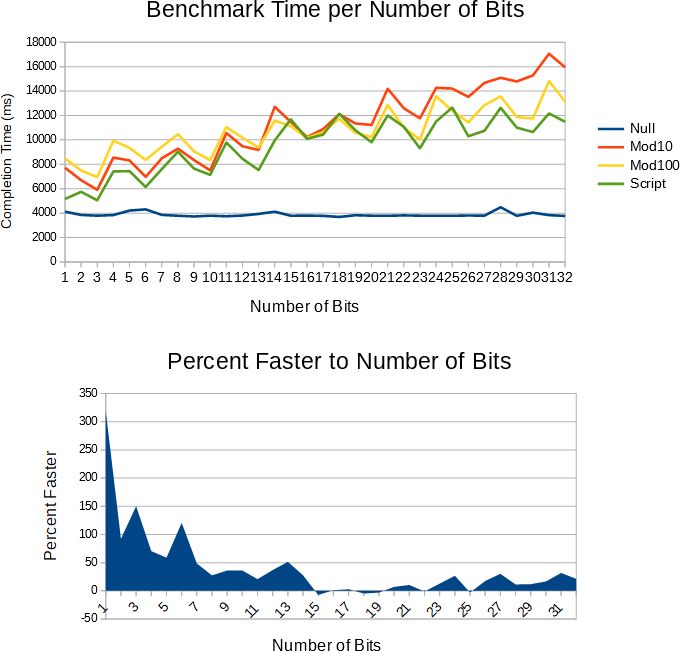
如需详细的记录和证明，请@see https://github.com/kabuki-starship/kabuki-toolkit/wiki/Fastest-Method-to-Align-Pointers。如果你想看看你为什么不应该使用modulo的证明，我发明了世界上最快的整数到字符串算法。本文的基准测试向您展示了优化一个模数指令的效果。请@see https://github.com/kabuki-starship/kabuki-toolkit/wiki/Engineering-a-Faster-Integer-to-String-Algorithm。

Answer 3

我正在编辑这个答案，因为：

我的原始代码中有一个错误（我忘记了intptr_t的类型转换），
我正在回答Jonathan Leffler的批评，以澄清我的意图。

下面的代码并不意味着您可以更改数组的值（foo）。但是你可以获得一个指向该数组的对齐指针，这个例子说明了一种方法。

#define         alignmentBytes              ( 1 << 2 )   // == 4, but enforces the idea that that alignmentBytes should be a power of two
#define         alignmentBytesMinusOne      ( alignmentBytes - 1 )

uint8_t         foo[ 1024 + alignmentBytesMinusOne ];
uint8_t         *fooAligned;

fooAligned = (uint8_t *)((intptr_t)( foo + alignmentBytesMinusOne ) & ~alignmentBytesMinusOne);

Answer 4

由于某种原因，我不能使用模或按位运算。在这种情况下：

void *alignAddress = (void*)((((intptr_t)address + align - 1) / align) * align) ;

对于C ++：

template <int align, typename T>
constexpr T padding(T value)
{
    return ((value + align - 1) / align) * align;
}
...
char* alignAddress = reinterpret_cast<char*>(padding<8>(reinterpret_cast<uintptr_t>(address)))

Answer 5

基于从其他地方学到的技巧，以及从阅读@par答案中得出的一个技巧，显然我在特殊情况下（对于像32位机器一样）所需要的全部是((size - 1) | 3) + 1，它的作用是这样的，以为对其他人可能有用，

for (size_t size = 0; size < 20; ++size) printf("%d\n", ((size - 1) | 3) + 1);

0
4
4
4
4
8
8
8
8
12
12
12
12
16
16
16
16
20
20
20

如何在C中对齐指针

5 个答案:

演示代码