k-表示具有质心约束

Question

我正在为数据科学课程的介绍开展一个数据科学项目，我们决定解决加利福尼亚海水淡化厂的问题：“我们应该把k植物放在哪里，以尽量减少邮政编码的距离？”

我们到目前为止的数据是，拉链，城市，县，流行，拉特，长，水量。

问题是，我找不到任何有关如何强制质心被限制在海岸上的资源。到目前为止我们想到的是： 使用普通的kmeans算法，但是一旦集群已经稳定，就将质心移动到海岸（坏） 使用具有权重的普通kmeans算法，使沿海拉链具有无限的权重（我被告知这不是一个很好的解决方案）

你们觉得怎么样？

Answer 1

我会通过设置可能成为中心的点来实现这一点，即你的海岸线 我认为这接近于Nathaniel Saul's第一条评论 这样，对于每次迭代，不是选择均值，而是通过接近群集来选择可能的集合中的点。

我已将条件简化为仅2个数据列（lon。和lat。），但您应该能够推断出这个概念。为简单起见，为了演示，我基于here的代码。

在这个例子中，紫色点是海岸线上的位置。如果我理解正确，最佳Coastline位置应如下所示：

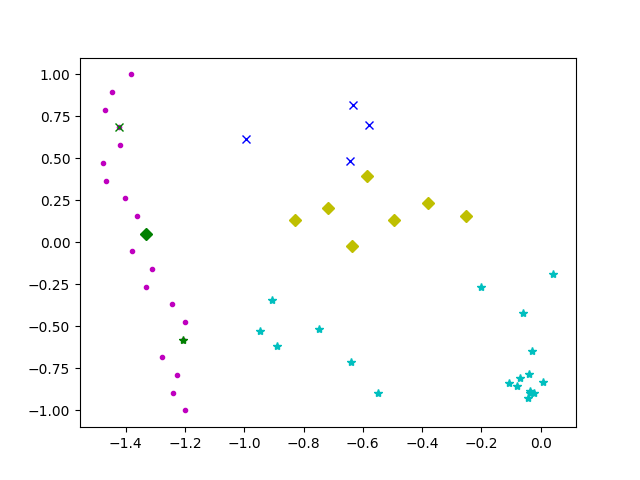
见下面的代码：

{{1}}

编辑以减少总距离。

Answer 2

K-means不会减少距离。

最小化平方错误，相当不同。 差异大致是中位数和1维数据中的平均值。错误可能是巨大的。

这是一个反例，假设我们有坐标：

-1 0
+1 0
 0 -1
 0 101

k-means选择的中心为0.25。最佳位置是0,0。 k均值的距离之和> 152，最佳位置有距离104.所以在这里，质心几乎比最佳位置差50％！但质心（=多元均值）是k-means使用的！

k-means不会使欧几里德距离最小化！

这是＆＃34; k-means对异常值敏感的一种变体＆＃34;。

如果你试图将它约束到中心并且＃34;它会变得更好。只在海岸上......

另外，你可能想要至少使用Haversine距离，因为在加利福尼亚州，北1度！= 1度以东，因为它不在赤道。

此外，您可能不假设每个位置都需要自己的管道，而是它们将像树一样连接。这大大降低了成本。

我强烈建议将此视为一般优化问题，而不是k-means。 K-means也是一种优化，但它可能会为您的问题优化错误的功能......