哪些类型可以区分类别？

Question

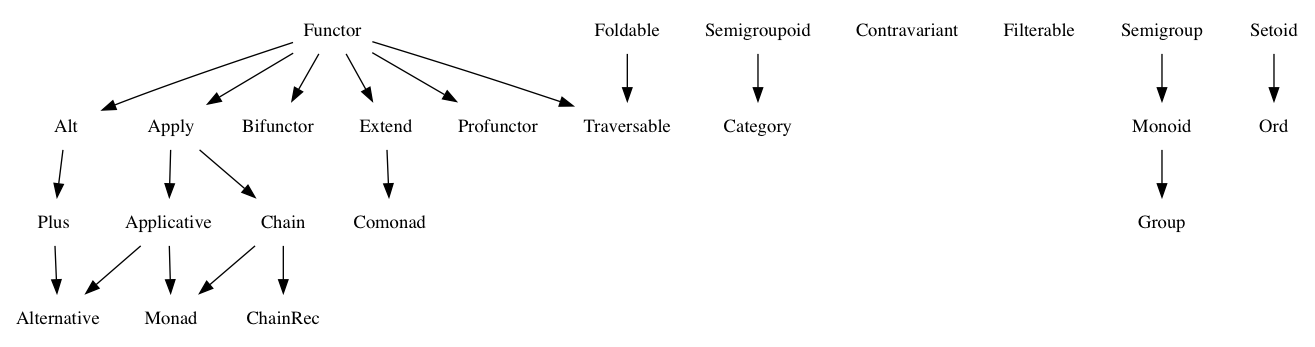
我仍然熟悉所有这些类别理论的东西，而且我看到的每个例子都是使用Maybe或Array。但我还没有找到任何区分这些类别的例子。例如，以下是我仍然无法回答的一些问题：

1. 什么是一个不是Monoid的半群？
2. 什么是可折叠的，也不是Traversable？ [Duplicate]
3. 什么是一个也不适用的Functor？
4. 什么也不是申请人？
5. 什么不是连锁店？
6. 什么链子不是Monad？
7. 什么样的申请人也不是Monad？ [Duplicate]

我通过JavaScript FantasyLand的语境学习这些东西，以便我从中获取语言 - 我知道这些东西有不同的词。

Answer 1

1。什么是半群而不是Monoid？

仙人掌给出了一个不是幺半群的半群的很好的例子。任何类型的非空（有限）列表代表该类型上的 free semigroup 。另一个示例是Data.Void.Void，它不是Monoid，因为它没有任何元素，因此没有标识元素。另一个例子是添加的正整数集。

3。什么是不是也适用的Functor？

不是Functor的{​​{1}} Apply为Handler。

data Handler a where
  Handler :: Exception e => (e -> IO a) -> Handler a

instance Functor Handler where
  fmap f (Handler h) = Handler (\e -> f <$> h e)

鉴于Handler f :: Handler (a -> b)和Handler g :: Handler a，您有

f :: e1 -> IO (a -> b)
g :: e2 -> IO a

e1和e2是（可能不同的）异常类型。您需要为某些例外类型h :: e3 -> IO b创建e3。没有真正明智的方法来做到这一点**。

似乎更难找到Functor 无法成为守法Apply实例，因为Apply只有一个法则，因此承认Applicative拒绝的各种奇怪的事情。

4。什么是申请也不是申请人？

6。什么是申请人，也不是Monad？

Map k和IntMap。此外，(,) a和Const a当a是Semigroup但不是Monoid时。同样，其他一些类型符合接受Apply和/或Bind的弱上下文的模式，而不是Applicative或Monad。

5。什么是申请，也不是一个链？

ZipList是Apply，但不是Bind。我不知道Chain是什么。

**一种半合理的方式可能如下：

data P x y = P x y deriving (Show, Typeable)
instance (Exception x, Exception y) =>
            Exception (P x y)
instance Apply Handler where
  Handler f <.> Handler g =
    Handler (\(P e1 e2) -> f e1 <*> g e2)

我认为这符合Apply法律，但我还不完全确定。

Answer 2

非空列表，定义为data NEList a = Cons a [a]是半群，但不是幺半群。