代表浮动到二进制

Question

所以我最近学会了将浮点数表示为二进制字符串的方法，我遇到了一个令人讨厌的混乱。

假设我有浮动10.25。在二进制中，这将是1010.01

取指数，这将是1.01001 x 2 ^（3）。 所以符号位为0，指数是127 + 3的无符号8位二进制， 这将成为10000010。 现在对于小数部分，这应该是00000000 00000000 0001001（23位）

全部放在一起，0 10000010 00000000 00000000 0001001。

但是当我把它放到转换网站时，它给了我这个： 看起来Mantissa部分已被每8位翻转，可能是因为小端实现。但事情就是这样。

来自Big Endian Mantissa 00000000 00000000 0001001，

Little Endian Mantissa不应该是10010000 00000000 0000000吗？

图像显示二进制字符串为0 10000010 0100100 00000000 00000000

Answer 1

正如你正确写的那样

• 标志为0
• 指数为10000010
• 尾数是01001000000000000000000（为了填补32位模式，添加了一些尾随的0＆＃39;）

将这些部分放在一起我们得到了

0 10000010 01001000000000000000000

现在，将这些位排列成字节，我们有

01000001 00100100 00000000 00000000

根据IEEE 754单精度格式，这正是10.25的表示。在大端机器中，4字节或如上所述，在小端机器中，它们是相反的。那是

• 10.25在大端机器上01000001 00100100 00000000 00000000
• 10.25 in little endian machines 00000000 00000000 00100100 01000001

IEEE 754 standard指定

• 第一位代表符号
• 接下来的8位代表指数
• 其余位代表尾数减1

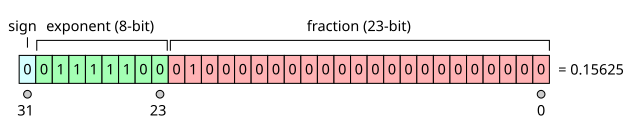
如果m1..m23是构成尾数的位，那么m1的重量为2 ^ -1，m23的重量为2 ^ -23。
简单来说，它是决定每一位含义的标准。