Question

对于lambda和beta-bar的隐式方程（命名为“y”），用“ezplot”命令绘制，我知道有可能通过像“二分法”这样的根查找算法，我可以找到解决方案每增加一个λ的β杆。但是如何构建这样的算法来正确获取线条。（我认为β条的解决方案应该在n * m矩阵中）你会一般地展示绘制这种问题的方法吗？谢谢。我的一个原因是我的等式的“ezplot”命令不连续。好的，这是我的照片： alt text http://www.mojoimage.com/free-image-hosting-view-05.php?id=5039TE-beta-bar-L-n2-.png

或 http://www.mojoimage.com/free-image-hosting-05/5039TE-beta-bar-L-n2-.png {
{3}} 和我的代码（简而言之）：

h=ezplot('f1',[0.8,1.8,0.7,1.0]);

和另一个m.file

function y=f1(lambda,betab)
n1=1.5; n2=1; z0=120*pi;
d1=1; d2=1;  a=1;
k0=2*pi/lambda;
u= sqrt(n1^2-betab^2);
wb= sqrt(n2^2-betab^2);
uu=k0*u*d1;
wwb=k0*wb*d2 ;
z1=z0/u;  z1_b=z1/z0;
a0_b=tan(wwb)/u+tan(uu)/wb;
b0_b=(1/u^2-1/wb^2)*tan(uu)*tan(wwb);
c0_b=1/(u*wb)*(tan(uu)/u+tan(wwb)/wb);
uu0= k0*u*a; m=0;
y=(a0_b*z1_b^2+c0_b)+(a0_b*z1_b^2-c0_b)*...
cos(2*uu0+m*pi)+b0_b*z1_b*sin(2*uu0+m*pi);
end

fzero找不到根;它说“功能价值必须是真实的和有限的”。无论如何，是否有可能消除不连续性并仅绘制y的实零？迄今为止，对于另一个功能（即fTE），它是：

function y=fTE(lambda,betab,s)
m=s;
n1=1.5;    n2=1;
d1=1;   d2=1;   a=1; 
z0=120*pi; 
k0=2*pi/lambda;
u = sqrt(n1^2-betab^2);  
w = sqrt(betab^2-n2^2);           
U = k0*u*d1;   
W = k0*w*d2 ;     
z1 = z0/u;             z1_b = z1/z0; 
a0_b = tanh(W)/u-tan(U)/w;
b0_b = (1/u^2+1/w^2)*tan(U)*tanh(W);
c0_b = -(tan(U)/u+tanh(W)/w)/(u*w);
U0 = k0*u*a;
y = (a0_b*z1_b^2+c0_b)+(a0_b*z1_b^2-c0_b)*cos(2*U0+m*pi)...
+ b0_b*z1_b*sin(2*U0+m*pi);
end

我用这些代码绘制了“y”的实数零：

s=0;  % s=0 for even modes and s=1 for odd modes.
lmin=0.8;       lmax=1.8;
bmin=1;            bmax=1.5;
lam=linspace(lmin,lmax,1000);
for n=1:length(lam)
    increment=0.001;  tolerence=1e-14; xstart=bmax-increment;
    x=xstart;
    dx=increment;
    m=0;   
    while x > bmin
        while dx/x >= tolerence
            if fTE(lam(n),x,s)*fTE(lam(n),x-dx,s)<0
                dx=dx/2;
            else
                x=x-dx;
            end
        end
        if abs(real(fTE(lam(n),x,s))) < 1e-6    %because of discontinuity some answers are not correct.%
            m=m+1;
            r(n,m)=x;
        end
        dx=increment;
        x=0.99*x;
    end
end
figure
hold on,plot(lam,r(:,1),'k'),plot(lam,r(:,2),'c'),plot(lam,r(:,3),'m'),
xlim([lmin,lmax]);ylim([1,1.5]),
xlabel('\lambda(\mum)'),ylabel('\beta-bar')

你看我使用矩阵来保存这个情节的数据。

！[alt text] [2] 因为这里的线条从左（轴）开始到严格。但如果第一行（上）从某个位置开始到某个位置（对于第一个数字和f1函数），那么我不知道如何使用矩阵。让我们改进这种方法。

[2]：Free Image Hosting
http://www.mojoimage.com/free-image-hosting-05/2812untitled.png

Answer 1

有时候EZPLOT会显示不连续性，因为确实存在不连续或某种形式的复杂行为。您可以使用CONTOUR函数以另一种方式生成绘图来查看此内容。

您应首先将arithmetic operators（f1，*和/）替换为元素等效项^来修改.*函数。 {1}}，./和.^），以便f1可以接受lambda和betab的矩阵输入。然后，运行以下代码：

lambda = linspace(0.8,1.8,500);  %# Create a vector of 500 lambda values
betab = linspace(0.7,1,500);     %# Create a vector of 500 betab values
[L,B] = meshgrid(lambda,betab);  %# Create 2-D grids of values
y = f1(L,B);                     %# Evaluate f1 at every point in the grid
[c,h] = contour(L,B,y,[0 0]);    %# Plot contour lines for the value 0
set(h,'Color','b');              %# Change the lines to blue
xlabel('\lambda');                                   %# Add an x label
ylabel('$\overline{\beta}$','Interpreter','latex');  %# Add a y label
title('y = 0');                                      %# Add a title

你应该看到以下情节：

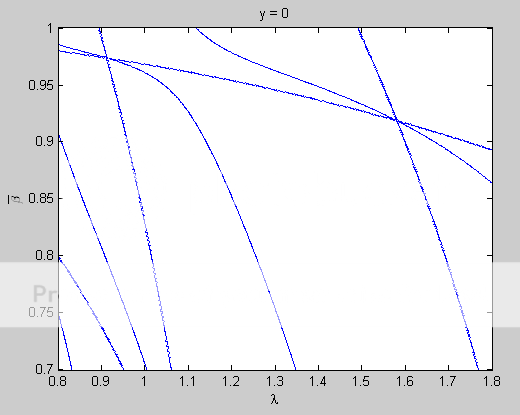
alt text

请注意，在使用EZPLOT时，图中现在有其他行没有出现，而且这些行非常锯齿状。您可以放大左上角的十字路口，并使用SURF制作一个情节，以了解正在发生的事情：

lambda = linspace(0.85,0.95,100);  %# Some new lambda values
betab = linspace(0.95,1,100);      %# Some new betab values
[L,B] = meshgrid(lambda,betab);    %# Create 2-D grids of values
y = f1(L,B);                       %# Evaluate f1 at every point in the grid
surf(L,B,y);                       %# Make a 3-D surface plot of y
axis([0.85 0.95 0.95 1 -5000 5000]);                 %# Change the axes limits
xlabel('\lambda');                                   %# Add an x label
ylabel('$\overline{\beta}$','Interpreter','latex');  %# Add a y label
zlabel('y');                                         %# Add a z label

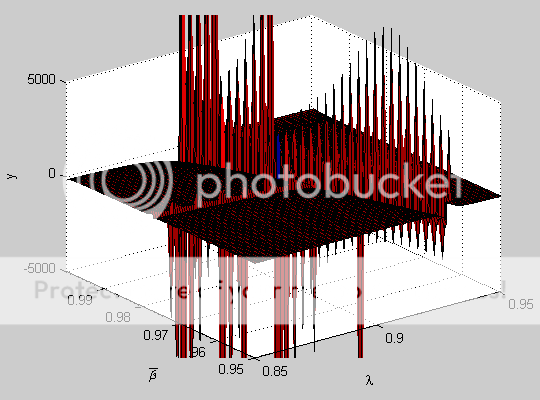
alt text

请注意，这些附加线上会发生很多高频周期性活动，这就是它们在等高线图中看起来如此锯齿的原因。这也是像EZPLOT这样的通用实用程序在那里显示中断的原因，因为它实际上并不是为了处理复杂和性能不佳的函数的特定情况。

编辑:(回复评论）

这些额外的行可能不是真正的过零点，尽管从SURF图中很难说出来。在这些线上可能存在不连续性，其中函数在线的一侧射出-Inf并且在线的另一侧射出Inf。渲染曲面或计算轮廓时，线的两侧的这些点可能会被错误地连接，从而产生沿线的零交叉的错误外观。

如果要在lambda的值下找到零交叉，可以尝试使用函数FZERO和anonymous function来转换两个变量的函数{{1转换为一个变量f1的函数：

fcn

也许矩阵图！

1 个答案: