确定一个集合与另外两个集合的交集是否为空

Question

对于任何三个给定的集合A，B和C：有没有办法确定（以编程方式）是否存在A的元素是B和C的连接（编辑：交集）的一部分？

例如：
答：所有大于3的数字 B：所有数字小于7
C：所有等于5的数字

在这种情况下，A组中有一个元素，即数字5，它适合。我将其作为规范实现，因此这个数值范围只是一个例子。 A，B，C可以是任何东西。

Answer 1

修改 谢谢Niki！

B.Count <= C.Count <= A.Count。

会有所帮助

D = GetCommonElements(B,C);
if( D.Count>0 && GetCommonElements(D,A).Count >0)
{
    // what you want IS NOT EMPTY
}
else
{
    // what you want IS EMPTY
}

SET GetCommonElements(X,Y)
{
    common = {}
    for x in X:
       if Y.Contains(x):
         common.Add(x);
    return common;
}

请看Efficient Set Intersection Algorithm。

---

我们可以使用distributive laws of sets

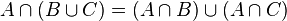
if(HasCommonElements(A,B) || HasCommonElements(A,C))
{
    // what you want IS NOT EMPTY
}
else
{
    // what you want IS EMPTY
}

bool HasCommonElements(X,Y)
{
    // if at least one common element is found return true(immediately)

    return false
}

Answer 2

如果我正确理解你的问题，你想要以编程方式计算3组的交集，对吧？您想要查看A中是否存在B和C交叉点中的元素，或者换句话说，您想知道A，B和C的交集是否为非空。

许多语言都设置了容器和交集算法，因此您应该只能使用它们。您在OCaml中的示例：

module Int = struct
    type t = int
    let compare i j = if i<j then -1 else if i=j then 0 else 1
end;;

module IntSet = Set.Make(Int);;

let a = List.fold_left (fun a b -> IntSet.add b a) IntSet.empty [4;5;6;7;8;9;10];;
let b = List.fold_left (fun a b -> IntSet.add b a) IntSet.empty [0;1;2;3;4;5;6];;
let c = IntSet.add 5 IntSet.empty;;

let aIbIc = IntSet.inter (IntSet.inter b c) a;;
IntSet.is_empty aIbIc;;

这输出false，因为b和c的交集是非空的（包含5）。这当然依赖于集合的元素具有可比性的事实（在示例中，函数比较在Int模块中定义了此属性）。

或者在C ++中：

#include<iostream>
#include<set>
#include<algorithm>
#include<iterator>

int main()
{
    std::set<int> A, B, C;

    for(int i=10; i>3; --i)
        A.insert(i);
    for(int i=0; i<7; ++i)
        B.insert(i);
    C.insert(5);

    std::set<int> ABC, BC;
    std::set_intersection(B.begin(), B.end(), C.begin(), C.end(), std::inserter(BC, BC.begin()));
    std::set_intersection(BC.begin(), BC.end(), A.begin(), A.end(), std::inserter(ABC, ABC.begin()));

    for(std::set<int>::iterator i = ABC.begin(); i!=ABC.end(); ++i)
    {
        std::cout << *i << " ";
    }
    std::cout << std::endl;

    return 0;
}

Answer 3

这个问题需要进一步澄清。 首先，你想使用范围给出的符号集吗？ 其次，这是一次性问题还是会以某种形式重复（如果是，问题的稳定部分是什么？）？

如果要使用范围，则可以使用二叉树表示这些范围，并在这些结构上定义联合和交叉操作。构建树将需要O（n log n）并且查找结果将需要O（log n）。仅使用树集不会得到回报，但是有效支持范围的任何组合都是灵活的（如果你认为'它可以是任何东西'）。

另一方面，如果任何意思，任何元素集，那么唯一的选择是枚举元素。在这种情况下，在集合B和C上构建B +树也将需要O（n log n）时间，但是这里n是元素的数量，并且在第一种情况下，n是范围的数量。后者可能会大几个数量级，当然它只能代表有限数量的元素。