在MATLAB中为球体表面的一个子集着色

Question

我正在尝试生成一个半球的图，表面上的阴影区域受到高程和方位角的最大/最小值的限制。基本上我正在尝试重现这个：

生成半球很容易，但过去我很难过。有什么想法吗？

这是我用来生成这个球体的代码：

[x,y,z] = sphere; 
x = x(11:end,:);
y = y(11:end,:); 
z = z(11:end,:);
r = 90; 
surf(r.*x,r.*y,r.*z,'FaceColor','yellow','FaceAlpha',0.5); 
axis equal;

Answer 1

一个选项是创建一个数组，其中包含您想要归属于每个点的相应颜色。

一个最小的例子（使用三角法将你的方位角和高程转换为x，y和z的逻辑条件）：

c=(y>0).*(x>0).*(z>0.1).*(z<0.5);
c(c==0)=NaN;
surf(r.*x,r.*y,r.*z,c ,'FaceAlpha',0.5); axis equal;

得出这个：

注意：这仅适用于网格的分辨率。 （即表面的每个贴片可以具有不同的颜色）。要精确地重现绘图，您可能希望将网格球体与另一个具有更多网格点的网格球体叠加，您可以在其上应用上述代码。

Answer 2

如果要突出显示半球的某个区域，首先要确定最小和最大方位角（水平扫描）和仰角（垂直扫描）角度。完成此操作后，请使用x,y,z坐标并将它们转换为球形坐标中的相应角度。完成后，您可以根据这些角度对x,y,z坐标进行子集化。要从笛卡儿转换为球形，您可以这样做：

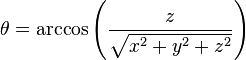
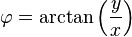
^{来源：Wikipedia}

theta是你的高程，phi是你的方位角。 r将是球体的半径。因为sphere生成单位范围的坐标r = 1。因此，要计算角度，我们只需要这样做：

theta = acosd(z);
phi = atan2d(y, x);

请注意，仰角/ theta被限制在0到180度之间，而方位角/ phi被限制在-180到180度之间。因为您只创建一半球体，所以高度应该在0到90度之间变化。另请注意，acosd和atan2d会将结果返回度。现在我们就在这里，您只需要对要绘制的球体的哪个部分进行子集化。例如，让我们说我们想限制球体，使得min。最多方位角从-90到90度，而仰角仅从0到45度。因此，让我们找到满足这些约束条件的x,y,z坐标，并确保将此范围之外的任何内容设置为NaN，以便这些点不会被显示在球体。就这样：

%// Change your ranges here
minAzimuth = -90;
maxAzimuth = 90;
minElevation = 0;
maxElevation = 45;

%// Compute angles - assuming that you have already run the code for sphere
%// [x,y,z] = sphere;
%// x = x(11:end,:);
%// y = y(11:end,:); 
%// z = z(11:end,:);
theta = acosd(z);
phi = atan2d(y, x);

%%%%%// Begin highlighting logic
ind = (phi >= minAzimuth & phi <= maxAzimuth) & ...
      (theta >= minElevation & theta <= maxElevation); % // Find those indices
x2 = x; y2 = y; z2 = z; %// Make a copy of the sphere co-ordinates
x2(~ind) = NaN; y2(~ind) = NaN; z2(~ind) = NaN; %// Set those out of bounds to NaN

%%%%%// Draw our original sphere and then the region we want on top
r = 90;
surf(r.*x,r.*y,r.*z,'FaceColor','white','FaceAlpha',0.5); %// Base sphere
hold on;
surf(r.*x2,r.*y2,r.*z2,'FaceColor','red'); %// Highlighted portion
axis equal;
view(40,40); %// Adjust viewing angle for better view

......这就是我得到的：

我已经使代码模块化，因此您所要做的就是更改代码开头定义的四个变量，输出将突出显示半球所需的部分最小和最大范围。

---

希望这有帮助！