Question

我知道如何制作Fibonacci数列表，但我不知道如何测试给定数字是否属于斐波那契列表 - 记住的一种方法是生成fib列表。数字达到那个数字并查看它是否属于数组，但必须有另一种更简单，更快速的方法。

有什么想法吗？

Answer 1

一个非常好的测试是当且仅当5 N^2 + 4或5N^2 – 4是平方数时，N是斐波那契数。有关如何有效地测试数字是正方形的想法，请参阅SO discussion。

希望这有帮助

Answer 2

当且仅当5ω² +4和5ω² - 4中的一个是完美平方时，正整数ω是斐波纳契数。

有关详情，请参阅The Faboulous Fibonacci Numbers。

alt text

Answer 3

虽然有几个人指出了完美平方的解决方案，但它涉及平均斐波那契数字，经常产生大量产品。

少于80个Fibonacci数字甚至可以保存在标准的64位整数中。

这是我的解决方案，它完全小比要测试的数字。< （用C＃编写，使用基本类型，如double和long。但算法应适用于更大的类型。）

static bool IsFib(long T, out long idx)
{
    double root5 = Math.Sqrt(5);
    double phi = (1 + root5) / 2;

    idx    = (long)Math.Floor( Math.Log(T*root5) / Math.Log(phi) + 0.5 );
    long u = (long)Math.Floor( Math.Pow(phi, idx)/root5 + 0.5);

    return (u == T);
}

<小时/> 在我写完这个答案4年多之后，一位评论者询问了out传递的第二个参数。

参数＃2是Fibonacci序列的“索引” 如果要测试的值T是斐波纳契数，那么idx将是斐波纳契数列中该数字的从1开始的索引。（有一个值得注意的例外）

Fibonacci序列为1 1 2 3 5 8 13等。
3是序列中的第4个数字：IsFib(3, out idx);将返回true和值4。
8是序列中的第6个数字：IsFib(8, out idx);将返回true和值6。
13是第7个数字; IsFib(13, out idx);将返回true和值7。

一个例外是IsFib(1, out idx);，它将返回2，即使值1出现在索引1和2处。

如果IsFib传递非斐波纳契数，它将返回false，idx的值将是最小斐波纳契数的索引，小于{{1} }。

16不是Fibonacci值。
T将返回IsFib(16, out idx);和值false。
您可以使用Binet's Formula将索引7转换为斐波纳契值13，这是最小的数字，小于16。

Answer 4

#!/bin/bash
victim="144"
curl http://aux.planetmath.org/files/objects/7680/fib.txt | sed 's/^[0-9]*//;s/[ \t]//g' | grep "^$victim$" >/dev/null 2>/dev/null
if [[ $? -eq 0 ]] ; then
    echo "$victim is a fibonacci number"
else
    echo "$victim aint"
fi

Answer 5

如果你的数字是有限大小的，而不是简单地将所有斐波那契数字放在哈希表的上限之下，测试包含就可以了。极少数的斐波那契数（例如，只有低于5毫升的38），因为它们呈指数增长。

如果您的数字不有限大小，那么建议的方形测试技巧几乎肯定比生成斐波纳契序列要慢，直到找到或超过该数字。

Answer 6

正整数ω是斐波那契数

当且仅当之一时 5ω² + 4和5ω² - 4是一个完美的正方形

来自 Alfred Posamentier和Ingmar Lehmann的（神话般的）FIBONACCI号码

bool isFibonacci(int  w)
{
       double X1 = 5 * Math.Pow(w, 2) + 4;
       double X2 = 5 * Math.Pow(w, 2) - 4;

       long X1_sqrt = (long)Math.Sqrt(X1);
       long X2_sqrt = (long)Math.Sqrt(X2);   

       return (X1_sqrt*X1_sqrt == X1) || (X2_sqrt*X2_sqrt == X2) ;
}

I copied it from this source

在1k和10k之间打印斐波那契数字的代码段。

for (int i = 1000; i < 10000; i++)
{
         if (isFibonacci(i))
              Console.Write(" "+i);
}

OMG只有四个 !!!

使用其他方法

from math import *

phi = 1.61803399
sqrt5 = sqrt(5)

def F(n):
    return int((phi**n - (1-phi)**n) /sqrt5)

def isFibonacci(z):
    return F(int(floor(log(sqrt5*z,phi)+0.5))) == z

print [i for i in range(1000,10000) if isFibonacci(i)]

Answer 7

寻求解决方案，看看Binet的公式。
（在维基百科上的Fibonacci Number下查找“封闭表达式”）

它说Fibonacci数的序列是由一个简单的闭合公式创建的：

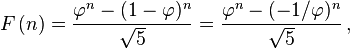
$alt text$

我相信如果您解决n，并测试n是否为整数，那么您将得到答案。

编辑正如@psmears指出的那样，同一篇维基百科文章也有关于检测斐波纳契数的部分。维基百科是一个很好的来源。

Answer 8

请参阅wikipedia article about the Fibonacci numbers上的“识别斐波纳契数字”部分。

Answer 9

由于斐波纳契数以指数方式增长，因此您建议的方法非常快。另一个是this。

Answer 10

基于我和psmears的早期答案，我已经编写了这个C＃代码。

它逐步完成这些步骤，并且可以明显地减少和优化：

// Input: T: number to test.
// Output: idx: index of the number in the Fibonacci sequence.
//    eg: idx for 8 is 6. (0, 1, 1, 2, 3, 5, 8)
// Return value: True if Fibonacci, False otherwise.
static bool IsFib(long T, out int idx)
{
    double root5 = Math.Sqrt(5);
    double PSI = (1 + root5) / 2;

    // For reference, IsFib(72723460248141) should show it is the 68th Fibonacci number

    double a;

    a = T*root5;
    a = Math.Log(a) / Math.Log(PSI);
    a += 0.5;
    a = Math.Floor(a);
    idx = (Int32)a;

    long u = (long)Math.Floor(Math.Pow(PSI, a)/root5 + 0.5);

    if (u == T)
    {
        return true;
    }
    else
    {
        idx = 0;
        return false;
    }
}

测试显示这适用于前69个斐波那契数字，但分解为第70个。

F(69) = 117,669,030,460,994 - Works
F(70) = 190,392,490,709,135 - Fails

总之，除非你使用某种BigInt库，否则最好有一个简单的Fibonacci数字查找表并检查它，而不是运行算法。

前300个号码列表随时可在线获取。

但是这段代码确实概述了一个可行的算法，只要你有足够的精度，并且不会溢出你的数字表示系统。

Answer 11

回复：艾哈迈德的代码 - 一种简单的方法，没有递归或指针，相当天真，但是对于任何不太真正的巨大数字都需要接下来没有计算能力（大约2N的补充来验证第N个纤维数，这在现代机器上最差的时候会花费几毫秒）

//如果找到任何内容则返回pos，如果没有则返回0（C / C ++处理任何值！= 0为真，因此结果相同）

int isFib (long n)
{
    int pos = 2;
    long last = 1;
    long current = 1;
    long temp;

    while (current < n)
    {
        temp = last;
        last = current;
        current = current + temp;
        pos++;
    }

    if (current == n)
        return pos;
    else
        return 0;

}

Answer 12

来自维基百科：http://en.wikipedia.org/wiki/Fibonacci_number

正整数z是斐波纳契数数字当且仅当5z ^ 2 + 4之一或5z ^ 2 - 4是一个完美的正方形。

Answer 13

Fibonacci数的一般表达式是 F（n）= [[（1 + sqrt（5））/ 2] sup n + 1 - [（1-sqrt（5））/ 2] sup n + 1] / sqrt（5）..... （*）第二个指数在大n时变为零并执行我们得到的数值运算F（n）= [（1.618）sup n + 1] / 2.236

如果K是要测试的数字，log（k * 2.2336）/ log（1.618）应该是一个整数！

K等于13的示例我的计算器给出答案7.00246 如果K等于14，答案是7.1564。

您可以通过获取最接近的整数来增加结果的置信度在（*）中回答并替换以确认结果为K

Answer 14

我在这里介绍的方法上运行了一些基准测试，还有简单的添加，预先计算数组，以及在哈希中记忆结果。对于Perl，至少，平方方法比对数方法快一点，可能快20％。正如abelenky指出的那样，在你是否有平均比特数的空间之间需要权衡。

当然，最快的方法是在域空间中散列所有Fibonacci数字。沿着abelenky所做的另一点，这些吸盘中只有94个小于2 ^ 64。

您应该预先计算它们，并将它们放在Perl哈希，Python字典或其他任何内容中。

Fibonacci数的属性非常有趣，但是使用它们来确定计算机程序中的某个整数是否与计算程序中的某个整数相似，就像每次程序启动时编写子程序来计算pi一样。

Answer 15

你要处理的数字有多大？

查找表可以为您工作吗？（您可以搜索的预先计算的数字列表）

还有一个closed-form expression，我想你可以反过来分析得到答案（虽然我不是数学家，所以我不能保证这个建议有意义）

Answer 16

这是我的解决方案我不确定它是否为基准。我希望这有帮助！

def is_fibonacci?(i)
  a,b=0,1
    until b >= i
        a,b=b,a+b
        return true if b == i
    end
end

a，b = b，a + b 正在做什么

 0, 1 = 1, 0 +1
 1, 1 = 1, 1 + 1
 1, 2 = 2, 1 + 2
 2, 3 = 3, 2 + 3

fib1 = fib2
fib2 = fib1 + fib2

Answer 17

Scala版本 -

def isFib(n: Int): Boolean = {

def checkFib(f1: Int = 1, f2: Int = 1): Boolean = {

if(n == f1 || n == f2) true
else if(n < f2) false
else checkFib(f2, f1+f2)

}

checkFib()

}

Answer 18

Java解决方案可以如下完成。但它仍然可以优化

以下解决方案适用于

1≤T≤10^ 5
1≤N≤10^ 10

T是测试用例的数量， N是数字范围

    import java.util.Scanner;
    import java.math.BigDecimal;
    import java.math.RoundingMode;

    public class FibonacciTester {
        private static BigDecimal zero = BigDecimal.valueOf(0);
        private static BigDecimal one = BigDecimal.valueOf(1);
        private static BigDecimal two = BigDecimal.valueOf(2);
        private static BigDecimal four = BigDecimal.valueOf(4);
        private static BigDecimal five = BigDecimal.valueOf(5);

        public static void main(String[] args) {
            Scanner sc = new Scanner(System.in);
            int n = sc.nextInt();
            BigDecimal[] inputs = new BigDecimal[n];
            for (int i = 0; i < n; i++) {
                inputs[i] = sc.nextBigDecimal();
            }

            for (int i = 0; i < inputs.length; i++) {
                if (isFibonacci(inputs[i]))
                    System.out.println("IsFibo");
                else
                    System.out.println("IsNotFibo");
            }


        }

        public static boolean isFibonacci(BigDecimal num) {
            if (num.compareTo(zero) <= 0) {
                return false;
            }

            BigDecimal base = num.multiply(num).multiply(five);
            BigDecimal possibility1 = base.add(four);
            BigDecimal possibility2 = base.subtract(four);


            return (isPerfectSquare(possibility1) || isPerfectSquare(possibility2));
        }

        public static boolean isPerfectSquare(BigDecimal num) {
            BigDecimal squareRoot = one;
            BigDecimal square = one;
            BigDecimal i = one;
            BigDecimal newSquareRoot;
            int comparison = -1;

            while (comparison != 0) {
                if (comparison < 0) {
                    i = i.multiply(two);
                    newSquareRoot = squareRoot.add(i).setScale(0, RoundingMode.HALF_UP);
                } else {
                    i = i.divide(two);
                    newSquareRoot = squareRoot.subtract(i).setScale(0, RoundingMode.HALF_UP);
                }

                if (newSquareRoot.compareTo(squareRoot) == 0) {
                    return false;
                }

                squareRoot = newSquareRoot;
                square = squareRoot.multiply(squareRoot);
                comparison = square.compareTo(num);
            }

            return true;
        }
    }

Answer 19

基本都给出了答案。我想添加一个非常快速的 C++ 示例代码。

基础是这里已经多次提到的查找机制。

使用比奈公式，我们可以计算出只有很少的斐波那契数适合 C++ unsigned long long 数据类型，现在到 2021 年通常是 64 位。大约 93。这在现在是非常低的号。

借助现代 C++ 17（及更高版本）功能，我们可以在编译时轻松为 64 位数据类型创建所有斐波那契数的 std::array。

因此，我们将只为查找数组花费 93*8= 744 BYTE 的非运行时内存。

然后使用 std::binary_search 查找值。所以，整个函数将是：

bool isFib(const unsigned long long numberToBeChecked) {
    return std::binary_search(FIB.begin(), FIB.end(), numberToBeChecked);
}

FIB 是编译时间，constexpr std::array。那么，如何构建该数组？

我们首先将计算斐波那契数的默认方法定义为 constexpr 函数：

// Constexpr function to calculate the nth Fibonacci number
constexpr unsigned long long getFibonacciNumber(size_t index) noexcept {
    // Initialize first two even numbers 
    unsigned long long f1{ 0 }, f2{ 1 };

    // Calculating Fibonacci value 
    while (index--) {
        // get next value of Fibonacci sequence 
        unsigned long long f3 = f2 + f1;
        // Move to next number
        f1 = f2;
        f2 = f3;
    }
    return f2;
}

这样，可以在运行时轻松计算斐波那契数。然后，我们用所有斐波那契数填充 std::array。我们还使用 constexpr 并使其成为带有可变参数包的模板。

我们使用 std::integer_sequence 为指数 0,1,2,3,4,5, .... 创建一个斐波那契数。

这很直接，并不复杂：

template <size_t... ManyIndices>
constexpr auto generateArrayHelper(std::integer_sequence<size_t, ManyIndices...>) noexcept {
    return std::array<unsigned long long, sizeof...(ManyIndices)>{ { getFibonacciNumber(ManyIndices)... } };
};

该函数将输入一个整数序列 0,1,2,3,4,... 并返回一个 std::array<unsigned long long, ...> 和相应的斐波那契数列。

我们知道最多可以存储 93 个值。因此我们创建了一个 next 函数，它将使用整数序列 1,2,3,4,...,92,93 调用上面的函数，如下所示：

constexpr auto generateArray() noexcept {
    return generateArrayHelper(std::make_integer_sequence<size_t, MaxIndexFor64BitValue>());
}

现在，终于，

constexpr auto FIB = generateArray();

会给我们一个名为 FIB 的编译时 std::array<unsigned long long, 93>，其中包含所有的斐波那契数。如果我们需要第 i 个斐波那契数，那么我们可以简单地写成 FIB[i]。运行时不会进行计算。

整个示例程序如下所示：

#include <iostream>
#include <array>
#include <utility>
#include <algorithm>
#include <iomanip>
// ----------------------------------------------------------------------
// All the following will be done during compile time

// Constexpr function to calculate the nth Fibonacci number
constexpr unsigned long long getFibonacciNumber(size_t index) noexcept {
    // Initialize first two even numbers 
    unsigned long long f1{ 0 }, f2{ 1 };

    // calculating Fibonacci value 
    while (index--) {
        // get next value of Fibonacci sequence 
        unsigned long long f3 = f2 + f1;
        // Move to next number
        f1 = f2;
        f2 = f3;
    }
    return f2;
}
// We will automatically build an array of Fibonacci numbers at compile time
// Generate a std::array with n elements 
template <size_t... ManyIndices>
constexpr auto generateArrayHelper(std::integer_sequence<size_t, ManyIndices...>) noexcept {
    return std::array<unsigned long long, sizeof...(ManyIndices)>{ { getFibonacciNumber(ManyIndices)... } };
};

// Max index for Fibonaccis that for an 64bit unsigned value (Binet's formula)
constexpr size_t MaxIndexFor64BitValue = 93;

// Generate the required number of elements
constexpr auto generateArray()noexcept {
    return generateArrayHelper(std::make_integer_sequence<size_t, MaxIndexFor64BitValue>());
}

// This is an constexpr array of all Fibonacci numbers
constexpr auto FIB = generateArray();

// All the above was compile time
// ----------------------------------------------------------------------


// Check, if a number belongs to the Fibonacci series
bool isFib(const unsigned long long numberToBeChecked) {
    return std::binary_search(FIB.begin(), FIB.end(), numberToBeChecked);
}

// Test
int main() {

    const unsigned long long testValue{ 498454011879264ull };

    std::cout << std::boolalpha << "Does '" <<testValue << "' belong to Fibonacci series?  --> " << isFib(498454011879264) << '\n';

    return 0;
}

使用 Microsoft Visual Studio Community 2019 版本 16.8.2 开发和测试

使用 gcc 10.2 和 clang 11.0.1 额外测试

语言：C++ 17

Answer 20

int isfib(int n /* number */, int &pos /* position */)
{
   if (n == 1)
   {
      pos=2;  // 1 1
      return 1;
   }
   else if (n == 2)
   {
      pos=3;  // 1 1 2
      return 1;
   }
   else
   {
      int m = n /2;
      int p, q, x, y;
      int t1=0, t2 =0;
      for (int i = m; i < n; i++)
      {
        p = i;
        q = n -p;    // p + q = n
        t1 = isfib(p, x);
        if (t1) t2 = isfib(q, y);
        if (t1 && t2 && x == y +1)
        {
           pos = x+1;
           return 1; //true
        }
      }
      pos = -1;
      return 0; //false
   }
}

这个怎么样？

Answer 21

#include <stdio.h>
#include <math.h>

int main()
{
int number_entered, x, y;

printf("Please enter a number.\n");
scanf("%d", &number_entered);
x = y = 5 * number_entered^2 + 4;        /*Test if 5N^2 + 4 is a square number.*/
x = sqrt(x);
x = x^2;
if (x == y)
{
        printf("That number is in the Fibonacci sequence.\n");
    }
x = y = 5 * number_entered^2 - 4;        /*Test if 5N^2 - 4 is a square number.*/
x = sqrt(x);
x = x^2;
if (x == y)
{
    printf("That number is in the Fibonacci sequence.\n");
}
else
{
    printf("That number isn't in the Fibonacci sequence.\n");
}
return 0;
}

这会有用吗？

测试一个数字是否是斐波那契

21 个答案: