Question

我正在使用Dundas地图，需要使用描绘某些数据的气泡来覆盖地图。我想在地图中添加形状以实现这一目标。我可以像这样添加一个三角形（或任何直线多边形）：

public static void AddShape(this MapControl map, List<MapPoint> points, Color color, string name)
{
    if (points[0].X != points[points.Count - 1].X && points[0].Y != points[points.Count - 1].Y)
        points.Add(points[0]);
    var shape = new Shape
    {
        Name = name,
        BorderColor = color,
        BorderStyle = MapDashStyle.Solid,
        BorderWidth = 1,
        Color = Color.FromArgb((int)(255 * (0.3)), color)
    };
    var segments = new[] {new ShapeSegment {Type = SegmentType.Polygon, Length = points.Count}};
    shape.AddSegments(points.ToArray(), segments);
    map.Shapes.Add(shape);
}

public static void AddBermudaTriangle(this MapControl map)
{
    var points = new List<MapPoint>
                     {
                         new MapPoint(-80.15, 26.0667),
                         new MapPoint(-64.75, 32.333),
                         new MapPoint(-66.07, 18.41)
                     };
    map.AddShape(points, Color.Red, "Bermuda Triangle");
}

Bermuda Triangle

你可以看到百慕大三角以红色覆盖地图。现在我想计算一组要传递给我的AddShape方法的点，该方法将绘制一个椭圆或圆。我只需要一个简单的算法来计算给定数量的点的x和y坐标。也许从一个代表圆心的特定点开始。例如：

public static void AddCircle(this MapControl map, Point centre, double radius, string name)
{
    var points = new List<MapPoint>();
    const int n = 360;
    for(var i = 0; i < n; i++)
    {
        //calculate x & y using n, radius and centre
        double x = 0;
        double y = 0;
        points.Add(new MapPoint(x, y));
    }
    map.AddShape(points, Color.Red, name);
}

我知道x，y计算是简单的三角函数，但我正在脑部冻结。救命啊！

编辑（使用tur！ng代码解决）：

public static void AddCircle(this MapControl map, Color color, MapPoint centre, double radius, string name)
{
    var points = new List<MapPoint>();
    const int n = 360;
    for(var i = 0; i < n; i++)
    {
        var x = (radius * Math.Cos(i * Math.PI / 180)) + centre.X;
        var y = (radius * Math.Sin(i * Math.PI / 180)) + centre.Y;
        points.Add(new MapPoint(x, y));
    }
    map.AddShape(points, color, name);
}

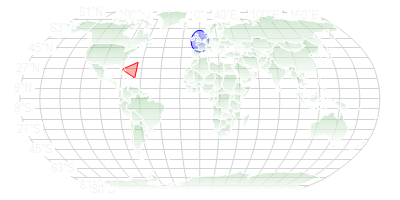
alt text

蓝色圆圈（在格林威治上空）由于罗宾逊网格上的地图投影而扭曲。

Answer 1

  double x = centre.x + radius*Math.cos(2*Math.PI/360 * i);
  double y = centre.y + radius*Math.sin(2*Math.PI/360 * i);

换一个圆圈。

Answer 2

从我很久以前写过的旧C ++程序复制而来，它仍然运行在几十个地方：

  // Approximate arc with small line segments
  double sa = dp[ix].center.angle(dp[ix].co);
  double ea = dp[ix].center.angle(dp[ix+1].co);
  double r = scale * dp[ix].radius;
  double rot = ea - sa;
  double inc = rot;
  if (dp[ix].dir == ROTCW) rot = -rot;
  if (rot < 0) rot += 2*PI;
  // Compute rotation increment that generates less than 1/4 pixel error
  if (r > 2) inc = 2*acos(1-0.25/r);
  if (inc >= rot || r < 2) addPoint(x, y);
  else {
    int cnt = int(1 + rot / inc);
    inc = rot / cnt;
    if (dp[ix].dir == ROTCW) inc = -inc;
    for (int jx = 0; jx < cnt; ++jx) {
      x = offsx + scale * dp[ix].center.x + r * cos(sa);
      y = offsy + scale * dp[ix].center.y + r * sin(sa);
      addPoint(x, y);
      sa += inc;
    }
  }

acos（）与Math.Acos（）相同。

Answer 3

回想一下圆的公式可以表示为

(x/r)**2 + (y/r)**2 = 1

其中x和y是坐标，r是半径。

椭圆的公式可以表示为

(x/a)**2 + (y/b)**2 = 1

其中a和b是半长轴和半轴（没有特定的顺序）。选择a和b为您提供“看起来不错”的椭圆。

您通常希望以相等的角度步长围绕圆圈选取您的点，以使真正的圆形更好看的多边形逼近。为此，您使用替换

x = r cos theta
y = r sin theta

并将你的循环从0运行到2 * pi。对于椭圆，您将使用

x = a cos theta
y = b sin theta

这将为您提供一个椭圆，其半长轴和半轴与X轴和Y轴平行，并以原点为中心。如果您想要一个具有任意位置的任意方向，您将需要以角度phi和平移来应用旋转。任何好的计算机图形文本都会为您提供必要的方程式，最有可能采用矩阵形式。

计算点以创建绘制椭圆的曲线或样条曲线

3 个答案: