如何在空间上重复排序组合

Question

很抱歉选择一个不具有表现力的标题但我无法想出更好的标题。

我正在寻找一种算法方式来查找重复组合，并按照以下方式在空间上对它们进行排序：

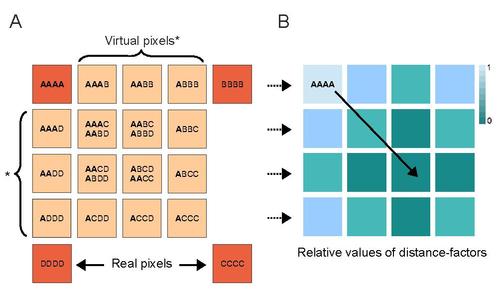
订单2（2x2）：

AA   AB 
AD AC/BD  

订单4（4x4）：

AAAA    AAAB     AABB    ABBB
AAAD AAAC/AABD AABC/ABBD ABBC
AADD AACD/ABDC ABCD/AACC ABCC
ADDD    ACDD     ACCD    ACCC

特别是那些双选项字段（例如AAAC / AABD）令我头疼。这些组合将用于计算真实像素之间的相关性。即例如，AA组合是A的自相关，而AB则是A和B的互相关。

这个方案是我目前试图实现的显微镜算法所必需的（参见交叉累积量部分）： http://en.wikipedia.org/wiki/Super-resolution_optical_fluctuation_imaging

除此之外，我还需要尽可能以最有效的方式执行此操作，因为我通常必须对数千张图像执行操作，每张图像至少为512x512（我在CUDA中执行此操作） ）。编辑：我刚刚意识到高效率并不是真正需要的，因为一旦订单被选中，模式就不会发生变化。

此图片可能有所帮助：

Answer 1

编辑：我在本页找到了一个用于平衡SOFI分析的MATLAB工具箱（在GNU公共许可下）：http://documents.epfl.ch/users/l/le/leuteneg/www/BalancedSOFI/index.html - 即使你不能使用MATLAB代码，也可以将它转换为你的编程语言。  

<小时/> 在维基百科文章的八篇参考文献中，有些是在付费墙之后，但是除了两篇最古老的文章之外，所有人都可以自由查看数字（或缩略图）。只有一篇文章可以免费访问类似维基百科（AAAB，AABB等）的数字：

http://www.opticsinfobase.org/boe/abstract.cfm?uri=boe-2-3-408

如果我在你的位置，我会尝试直接联系该论文的作者并询问他们的数字意味着什么，因为我没有看到他们如何决定使用这些组合。在3x3插值像素集中，由四个角上的像素A，B，C，D对称地限制，为什么A是每个组合中唯一需要出现的字母？如果我理解字母表示的是什么（每个插值像素的值中真实像素的相对权重），那么标记为ABCD AACC的对角线交叉点上的像素给予A和C两倍于B和D的权重;实际上，平均而言，整个3x3像素块的A和C的重量是B和D的两倍。这似乎与问题的基本对称性不一致。

Answer 2

你提供的wiki链接中的数学（关于超分辨率光学波动成像）可能需要我进行相当多的研究才能理解，但我观察到至少有一种可能的方法来考虑图A：

我认为A是一个锚点，向量可以从B，C和D延伸到A。直接向量可能相当明显 - 当我们从D直接向D移动时，A会累积（即AAAD，AADD，ADDD）;与B到A和C到D一样。

我将中间组合视为从边框水平或垂直延伸的向量。例如，从AAAB下来，我们添加一个C，然后添加另一个C;从AADD向右走，我们添加一个{{1}}，然后到达中间，ABCD。

我认为图中的任何一个组合都按字母顺序排序，这可以解释某些累积位置的明显差异，例如，从ADDD转移到ACCC时累积{{1}}的位置，比较从ABBB搬到ACCC时，积累“C”的位置。