编程基于数学的图像，用于高分辨率图稿

Question

我有兴趣创建包含重复模式的海报大小的图像，类似于下面的两个（公共领域）图像，Flower of Life和Penrose tiling：

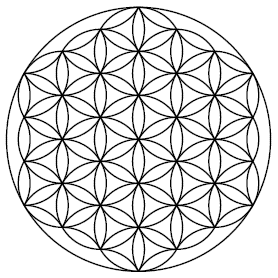
我的问题：

1. 人们通常如何在计算机上创建这样的图像？我希望答案不是“打开Adobe Illustrator并猜测交叉点”，因为这些点可以用数学方法定义。但我也想象不是每个对几何图案感兴趣的人都熟悉编程。
2. 创建此类图像的最佳环境是什么？特别是，从Java，Python，Processing等获取高分辨率图像的最佳方法是什么？或者，Mathematica是最好的工具吗？

在我看来，实际上计算得分并进行数学计算并不是困难的部分（至少，它不是这个问题的重点）。 我对从程序中获取高质量视觉产品的最佳方式感兴趣。

Answer 1

创建这样的图像的最佳方法是学习编写PostScript。这是一种干净的语言，易于学习，并且一旦你熟悉它就会非常强大。

Bill Casselman的manuals是迄今为止高质量数学插图的最佳参考。

Answer 2

使用像SVG这样的矢量图像格式。这将完美地扩展到任何分辨率。

Inkscape是创建这些内容的绝佳工具。

一旦有了矢量图像格式，在编程语言中有很多选择，具体取决于您选择的语言。

例如 -

• .NET - SvgNet
• ActionScript - svgweb
• C ++ - LeadTools
• 适用于WPF / Silverlight的XAML - ViewerSVG（将SVG转换为XAML）

Answer 3

嗯，＃2将是一场神圣的战争，所以我将解决＃1问题。 ：）

这种性质的图像的关键是递归。基本上它们是以受控方式一遍又一遍地重复的相同图像以获得有趣的结果。以生命之花为例。你重复中心花瓣六次（做花瓣的方法取决于你）。然后用花瓣尖端作为中心并重叠其中一个花瓣，再制作六朵花。然后你递归地向外移动。经过几次“回合”后，您将停止并绘制包含的圆圈。基本上，如果您手动操作，则可以模拟印记，移动和旋转。

当我玩这些东西时，我总是发现实验是获得酷炫新事物的最佳方式。当然，这可能只是我缺乏想象力。 ：）

我知道在这个答案中我的数学不是很重，但这取决于你和实验。请记住，COS和SIN是你的朋友，并且有三度的360度（或2pi弧度，取决于你的数学包）。

编辑：为“花”添加一些数学

从（Xo，Yo）的中心开始，花的半径为r ......

花瓣的尖端（P0，P1等）由......确定。

X = Xo + (sin((n * pi)/3 + (pi / 6)) * r)
Y = Yo - (cos((n * pi)/3 + (pi / 6)) * r)

其中n是花瓣数（0..5）

计算出花瓣尖后，只需绘制花瓣，然后在尖端开始新花。您还可以设置一个边界圆，以便不会绘制该圆外的任何点。

Answer 4

我不知道这些图像是如何创建的，我猜它们是从一本书中扫描出来的，但是，在我的分形工作中，我倾向于从使用<canvas>标签开始，主要是这样我可以改变元素的大小并看到它绘制更多的迭代，所以我可以得到最高的分辨率。

这就像SVG之类的问题是你需要选择一个分辨率然后创建它，并且它会向上和向下扩展，但是如果你以一个分辨率开发它，那么你会得到更高的分辨率为了演示，你可能会看到比你想要的更多的空白。

如果您想要将其保存为静态图像，那么任何GUI都可以正常工作，因为您在此时保存了GIF，但是如果您想要它，例如，在网页上，并拥有它在浏览器上看起来尽可能好，然后你可能想看看使用javascript。

数学部分并不难，因此一旦获得所需的递归算法，绘制图像就相当容易了。我倾向于进行下一次迭代，直到尺寸低于阈值，例如半径<1。 3，然后退出。

Answer 5

我会尝试使用Java中的iText创建PDF。 PDF支持矢量图形，因此它应该可以毫无问题地扩展。我不知道iText如何很好地扩展w.r.t.当你有大量的图形元素时表现。

Answer 6

A1。你可能想看看龟图形，l系统，迭代函数系统，空间填充曲线，以及可能还有许多我不熟悉或者还没有想过的其他方法。

A2。您可以使用您建议的任何语言对这些语言进行编程。我喜欢Mathematica，但我知道不是每个人都有它的副本我有一个副本'因为我在数字处理工作，并用它来制作漂亮的图片。但处理是免费的，旨在使艺术家友好，可能是一个更好的起点。 Mathematica和Processing都在那里做图形，然后没有调用外部库（或担心使用哪些）。

而且，虽然我同意每个说过矢量是要走的路的人，但不要忘记最后的制作步骤，纸张或屏幕上的渲染，所以要考虑如何完成。例如，这可能会导致您使用Postscript或PDF作为输出格式。

玩得开心

标记

Answer 7

好吧，我曾经用指南针绘制生活的花朵，然后在初中时......真的很简单......但我认为这不是你想要的答案。

基本上它包括从每个点绘制一个相同半径的圆，直到遇到大圆（极限）。