{0,1}上的序列数,使得序列至少包含一半
如何计算{0,1}上的序列数,使每个序列至少包含一半?
3 个答案:
答案 0 :(得分:5)
长度为n的序列总数为2 ^ n。如果n是奇数,那么它们的一半(2 ^(n-1))至少有一半。 对于偶数n,你必须考虑到n!/((n / 2)!^ 2)序列恰好有一半。所以在这种情况下,我认为你总有 (1/2)*(2 ^ n + n!/((n / 2)!^ 2))。
答案 1 :(得分:1)
假设序列的总长度为n,并且包含n / 2的序列的数量为:
n!/((n/2)!^2)
编辑:
抱歉,我犯了一个错误。我的意思是n!/((n/2)!^2)但不是n!/(2*(n/2)!)。我认为它是combination个问题并使用了以下公式。 (将k替换为n/2)
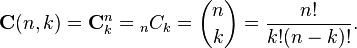
答案 2 :(得分:0)
编辑:当!我们(I)应该经常仔细阅读问题! 以下涉及枚举0和1的数量相等的序列数!实际问题是零的数量应该小于或等于1的数量!!!
Pierr的公式, n!/(2 *(n / 2)!)几乎是正确的,实际上是 n!/((n / 2)!*(n / 2)!)
但这可以使用一些解释(双关语;-))。
n是总长度,我们知道 n必须是偶数,因为问题需要相同数量的0和1。
让我们专注于放置0 。对于长度为n的序列,我们有 n / 2个零位,以放入序列的n个位置之一。我们只需要计算零位,因为在那之后就没有关于一位的选择:所有其他位置都需要1位。
所以... n / 2个零位,对于n个位置 ...有n种方法可以选择第一个位置,然后(n-1)个方法来选择第二个位置(两位不能占据相同的位置)等。 因此,这个选择数量是
n! / (n/2)!
例如,对于n = 6,我们有
6 * 5 * 4 choices,
which, by multiplying and dividing by (3*2*1) is equivalent to
= 6 * 5 * 4 * (3 * 2 * 1) / (3 * 2 * 1)
= 6! / 3!
= n! / (n/2)! (a)
现在......其中一些选择[在哪里放置第一位,第二位等],导致相同的组合,因为所有零位都是相同的,因此是否一个把位置x中的“第一”位和位置y中的“第二”位,或第一位称为y,第二位称为x,我们将具有相同的组合。有(n / 2)!排列这些n / 2位的方法。在n = 6的示例中,有3种方式选择“第一”位的位置,第2位的2种方式和最后的0位的1种(即无选择)。那么完整的公式需要是(a)除以(n / 2)!,即:
n! / (n/2)! * 1/(n/2)!
= n! / ((n/2)! * (n/2)!)
- 我写了这段代码,但我无法理解我的错误
- 我无法从一个代码实例的列表中删除 None 值,但我可以在另一个实例中。为什么它适用于一个细分市场而不适用于另一个细分市场?
- 是否有可能使 loadstring 不可能等于打印?卢阿
- java中的random.expovariate()
- Appscript 通过会议在 Google 日历中发送电子邮件和创建活动
- 为什么我的 Onclick 箭头功能在 React 中不起作用?
- 在此代码中是否有使用“this”的替代方法?
- 在 SQL Server 和 PostgreSQL 上查询,我如何从第一个表获得第二个表的可视化
- 每千个数字得到
- 更新了城市边界 KML 文件的来源?