红黑树 - 黑色高度限制

Question

我正在阅读关于Red-Black Trees的维基。

有人可以详细说明第5条限制：

  

  

1. 节点为红色或黑色。

  

2. 根是黑色的。

  

3. 所有叶子（NIL）都是黑色的。 （所有叶子的颜色与根相同。）

  

4. 每个红色节点的两个孩子都是黑色的。

  

5. 从给定节点到其任何后代叶子的每条简单路径都包含相同数量的黑色节点。

  

我很难理解它，因为在the final case of insertion（wiki上的案例5）之后给出了示例RBT的状态给了我们：

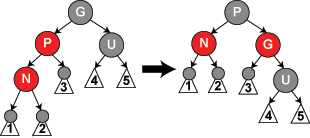
4和5是否有比1,2和3更多的黑色节点？

Answer 1

1,2,3,4和5都是子树。我们知道树1,2和3中根节点的颜色是黑色。我们不知道节点1-5中的任何节点是否是叶子节点，因为这种插入的情况可能是在新插入的节点（来自插入案例3）的祖父母的某些N上递归调用的。

在旋转之前和之后，子树1,2和3都低于一个黑色节点（G之前，P之后），而子树4和5低于两个黑色节点（之前是G和U，之后是P和U） 。子树1,2和3每个都有一个黑色节点而不是子树4和5。

Answer 2

我只是深入阅读，似乎图片有问题。

由于N是刚刚插入的节点，因此意味着在insert下P之前有子节点[1,3]或[2,3]（和插入件分别为2或1）。所以在这种情况下，在最后一次插入P和U之前必须是红色（并且4,5是黑色）。

Answer 3

祝贺James破译维基图！这没有错，只是含糊不清。

页面的“对话”标签提到“三角形并不代表树叶而是子树。有些子树的顶部有黑圈表示它们的根必须是黑色。”

显然，缺少圆圈的三角形表示根节点的颜色和树深度未知的子树（包括叶子）（并且可能是不相关的）。

因此，图表根本没有提供足够的信息来判断是否违反了“规则5”。我们必须把它作为一个给定的，但事实并非如此。