使用互相关比较2个信号时，什么是“好的”R值？

Question

我为提前有点冗长而道歉：如果你想跳过所有背景，你可以在下面看到我的问题。

这几乎是我之前发布的关于如何比较两个1D（时间相关）信号的问题的后续跟进。我得到的答案之一是使用互相关函数（MATLAB中的xcorr），我做了。

背景资料

也许一些背景信息会很有用：我正在尝试实现独立分量分析算法。我的一个非正式测试是（1）通过（a）生成2个随机向量（1x1000）来创建测试用例，（b）将向量组合成2x1000矩阵（称为“S”），并将其乘以2x2混合矩阵（称为“A”），给我一个新的矩阵（我们称之为“T”）。

总结：T = A * S

（2）然后我运行ICA算法生成混合矩阵的逆（称为“W”），（3）将“T”乘以“W”以（希望）给我重建原始信号矩阵（称为“X”）

总结：X = W * T

（4）我现在要比较“S”和“X”。虽然“S”和“X”是2x1000，但我只是将S(1,:)与X(1,:)和S(2,:)与X(2,:)进行比较，每个为1x1000，使其成为1D信号。 （我还有另一个步骤，确保这些矢量是相互比较的合适矢量，我也将信号归一化）。

所以我当前的困境是如何“评分”S(1,:)与X(1,:)的匹配程度，以及S(2,:)与X(2,:)的匹配程度。

到目前为止，我使用了类似：r1 = max(abs(xcorr(S(1,:), X(1,:)))

的内容

我的问题

假设使用互相关函数是比较两个信号的相似性的有效方法，那么对于信号的相似性进行分级将被认为是一个好的R值？维基百科说这是一个非常主观的领域，所以我推迟对那些可能在这个领域有经验的人做出更好的判断。

正如你可能已经意识到的那样，我根本不是来自EE / DSP /统计背景（我是一名医学院学生），所以我现在正在经历一场“火灾洗礼”，而我感谢我能得到的所有帮助。谢谢！

Answer 1

（编辑，直至回答有关R值的问题，请参阅下文）

解决这个问题的一种方法是使用互相关。请记住，您必须对幅度进行标准化并校正延迟：如果您有信号S1，并且信号S2的形状相同，但幅度减半并延迟3个样本，则它们仍然完全相关。

例如：

>> t = 0:0.001:1;
>> y = @(t) sin(10*t).*exp(-10*t).*(t > 0);
>> S1 = y(t);
>> S2 = 0.4*y(t-0.1);
>> plot(t,S1,t,S2);

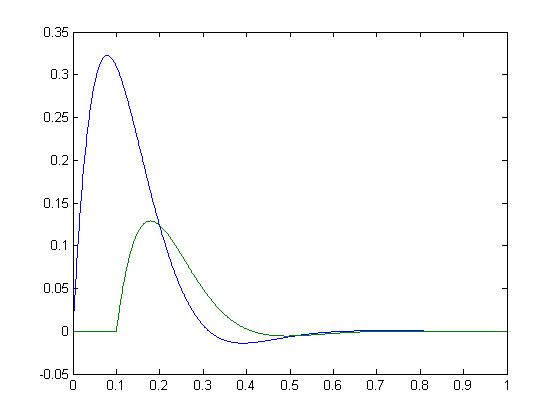
这些应具有完美的相关系数。计算它的一种方法是使用最大互相关：

>> f = @(S1,S2) max(xcorr(S1,S2));

f = 

    @(S1,S2) max(xcorr(S1,S2))

>>  disp(f(S1,S1)); disp(f(S2,S2)); disp(f(S1,S2));
   12.5000

    2.0000

    5.0000

xcorr()的最大值负责信号之间的时间延迟。至于校正振幅，您可以对信号进行归一化，使其自相关相关为1.0，或者您可以将该等效步骤折叠为以下内容：

ρ ² = f（S1，S2） ² /（f（S1，S1）* f（S2，S2）;

在这种情况下，ρ ² = 5 * 5 /(12.5 * 2）= 1.0

你可以求解ρ本身，即ρ= f（S1，S2）/ sqrt（f（S1，S1）* f（S2，S2）），请记住1.0和-1.0都是完全相关的（-1.0有相反的符号）

尝试使用你的信号！

---

关于接受/拒绝使用的阈值，这实际上取决于您拥有的信号类型。 0.9及以上版本相当不错，但可能会产生误导。我会考虑在减去相关版本后查看剩余信号。您可以通过查看xcorr（）的最大值的时间索引来执行此操作：

>> t = 0:0.001:1;
>> y = @(a,t) sin(a*t).*exp(-a*t).*(t > 0);
>> S1=y(10,t);
>> S2=0.4*y(9,t-0.1);
>> f(S1,S2)/sqrt(f(S1,S1)*f(S2,S2))

ans =

    0.9959

对于相关性来说，这看起来非常好。但是让我们尝试用S2的缩放/移位倍数拟合S2：

>> [A,i]=max(xcorr(S1,S2)); tshift = i-length(S1);
>> S2fit = zeros(size(S2)); S2fit(1-tshift:end) = A/f(S1,S1)*S1(1:end+tshift);
>> plot(t,[S2; S2fit]); % fit S2 using S1 as a basis

>> plot(t,[S2-S2fit]);  % residual

剩余有一些能量;为了感受多少，你可以使用它：

>> S2res=S2-S2fit;
>> dot(S2res,S2res)/dot(S2,S2)

ans =

    0.0081

>> sqrt(dot(S2res,S2res)/dot(S2,S2))

ans =

    0.0900

这表示残差具有原始信号S2的能量的约0.81％（均方根振幅的9％）。 （1D信号与其自身的点积将始终等于该信号与其自身的互相关的最大值。）

我认为回答两个信号彼此之间的相似之处并不是一个灵丹妙药，但希望我已经给了你一些可能适合你情况的想法。

Answer 2

一个好的起点是通过计算每个信号的自相关来了解完美匹配的样子（即做“交叉” “每个信号与自身的相关性”。

Answer 3

这是一个完整的GUESS - 但我猜最大（abs（xcorr（S（1，:)，X（1，:)）））＆gt; 0.8意味着成功。出于好奇，你得到什么样的价值max（abs（xcorr（S（1，:)，X（2，:)）））？

验证算法的另一种方法可能是比较A和W.如果W计算正确，它应该是A ^ -1，那么你可以计算像| A*W - I |这样的度量吗？也许你必须通过A*W的追踪来规范化。

回到原来的问题，我来自DSP背景，因此我可以处理相当无噪音的信号。我明白这不是你在生物学中获得的奢侈品:)所以我的0.8猜测可能会非常乐观。也许看一下你所在领域的一些文献，即使他们没有完全使用互相关，也许是有用的。

Answer 4

通常在这种情况下，人们会谈论“错误接受率”和“错误拒绝率”。 第一个描述算法对非相似信号说“相似”的次数，第二个是相反的。

因此，选择阈值将成为这些标准之间的权衡。要使FAR = 0，阈值应为1，使FRR = 0阈值应为-1。

很可能，您需要决定在您的情况下FAR和FRR之间的平衡是否可以接受，这将为阈值提供正确的值。

在数学上，这可以用不同的方式表达。只是几个例子： 1.将一些费率固定在可接受的价值，并尽量减少其他费率 2.最小化（FRR，FAR） 3.最小化 FRR + b FAR

Answer 5

由于它们应该相等，因此相关系数应该很高，在.99和1之间。我也会将max和abs函数从你的计算中拿出来。

编辑： 我说得太早了。我把互相关与相关系数混淆了，这是完全不同的。我的答案可能不值得。

Answer 6

我同意结果是主观的。那些涉及差异的平方和，逐个元素的东西会有一些价值。两个相同的数组将以该形式给出值0。你必须决定什么价值变得“糟糕”。组成两个“不太差”的不同矢量，找出它们的互相关系数作为指导。

（括号：如果你做的是相关系数，其中1或-1会很好而0会很糟糕，生物统计学家告诉我，真实值0.7非常好。我理解这不是你正在做的事情，但相关系数的评论提前出现了。）