用于计算百分位数以移除异常值的快速算法

Question

我有一个程序需要重复计算数据集的近似百分位数（订单统计数据），以便在进一步处理之前删除异常值。我目前正在通过对值数组进行排序并选择适当的元素来实现这一目标;这是可行的，但尽管这是该计划的一个相当小的部分，但它在个人档案中是一个值得注意的昙花一现。

更多信息：

• 数据集包含最多100000个浮点数的数量级，并假设“合理”分布 - 在特定值附近不太可能出现重复，密度也不大;如果由于某种奇怪的原因，分布是奇数，那么近似值就不太准确了，因为数据可能无论如何都搞砸了并且进一步处理可疑。但是，数据不一定是统一的或正态分布的;它不太可能退化。
• 近似解决方案没问题，但我确实需要了解 近似值如何引入错误以确保其有效。
• 由于目标是删除异常值，我在任何时候都在同一数据上计算两个百分点：例如一个是95％，一个是5％。
• 该应用程序位于C＃中，在C ++中有点繁重;任何一个伪代码或预先存在的库都可以。
• 一种完全不同的去除异常值的方法也可以，只要它是合理的。
• 更新： 我似乎正在寻找近似selection algorithm。

尽管这一切都是在一个循环中完成的，但每次数据都会略微不同，因此重用数据结构并不像for this question那样容易。

已实施解决方案

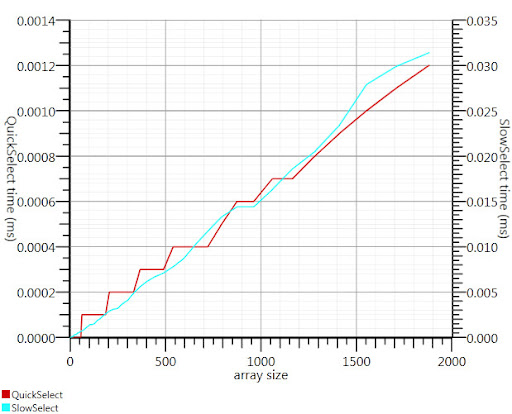
使用Gronim建议的维基百科选择算法将这部分运行时间减少了大约20倍。

由于我找不到C＃实现，这就是我想出的。即使对于小型输入，它也比Array.Sort更快;在1000个元素上它的速度提高了25倍。

public static double QuickSelect(double[] list, int k) {
    return QuickSelect(list, k, 0, list.Length);
}
public static double QuickSelect(double[] list, int k, int startI, int endI) {
    while (true) {
        // Assume startI <= k < endI
        int pivotI = (startI + endI) / 2; //arbitrary, but good if sorted
        int splitI = partition(list, startI, endI, pivotI);
        if (k < splitI)
            endI = splitI;
        else if (k > splitI)
            startI = splitI + 1;
        else //if (k == splitI)
            return list[k];
    }
    //when this returns, all elements of list[i] <= list[k] iif i <= k
}
static int partition(double[] list, int startI, int endI, int pivotI) {
    double pivotValue = list[pivotI];
    list[pivotI] = list[startI];
    list[startI] = pivotValue;

    int storeI = startI + 1;//no need to store @ pivot item, it's good already.
    //Invariant: startI < storeI <= endI
    while (storeI < endI && list[storeI] <= pivotValue) ++storeI; //fast if sorted
    //now storeI == endI || list[storeI] > pivotValue
    //so elem @storeI is either irrelevant or too large.
    for (int i = storeI + 1; i < endI; ++i)
        if (list[i] <= pivotValue) {
            list.swap_elems(i, storeI);
            ++storeI;
        }
    int newPivotI = storeI - 1;
    list[startI] = list[newPivotI];
    list[newPivotI] = pivotValue;
    //now [startI, newPivotI] are <= to pivotValue && list[newPivotI] == pivotValue.
    return newPivotI;
}
static void swap_elems(this double[] list, int i, int j) {
    double tmp = list[i];
    list[i] = list[j];
    list[j] = tmp;
}

谢谢，Gronim，指出我正确的方向！

Answer 1

Henrik的直方图解决方案将起作用。您还可以使用选择算法有效地找到O（n）中n个元素数组中的k个最大或最小元素。要将其用于第95百分位数集k = 0.05n并找到k个最大元素。

参考：

http://en.wikipedia.org/wiki/Selection_algorithm#Selecting_k_smallest_or_largest_elements

Answer 2

According创建者SoftHeap可用于：

  

计算精确或近似中位数   并且百分位数最佳。也是   适用于近似排序...

Answer 3

您可以从数据集的一部分估算百分位数，例如前几千点。

如果您可以假设您的数据点是独立的，那么Glivenko–Cantelli theorem可以确保这是一个相当不错的估计值。

Answer 4

我曾经通过计算standard deviation来识别异常值。距离平均值超过标准偏差2倍（或3倍）的距离都是异常值。 2次=约95％。

由于你正在计算平均值，所以它也很容易计算出标准偏差非常快。

您也可以只使用数据的一个子集来计算数字。

Answer 5

将数据的最小值和最大值之间的间隔划分为（例如）1000个二进制数并计算直方图。然后构建部分总和并查看它们首次超过5000或95000的位置。

Answer 6

我能想到几种基本方法。首先是计算范围（通过查找最高值和最低值），将每个元素投影到百分位数（（x - min）/范围）并抛弃任何评估低于.05或高于.95的值。

第二个是计算平均值和标准差。与平均值（在两个方向上）的2个标准偏差的跨度将包围95％的正态分布的样本空间，这意味着您的异常值将在＆lt; 2.5和＆gt; 97.5百分位数中。计算一系列的平均值是线性的，标准dev（每个元素的差值和均值之和的平方根）也是如此。然后，从平均值中减去2个sigmas，并将平均值加2 sigmas，你就得到了异常值。

这两个都将在大致线性时间内计算;第一个需要两个通过，第二个需要三个（一旦你有你的限制，你仍然需要丢弃异常值）。由于这是一个基于列表的操作，我认为你不会发现任何具有对数或常数复杂性的东西;任何进一步的性能提升都需要优化迭代和计算，或者通过对子样本（例如每三个元素）执行计算来引入错误。

Answer 7

对您的问题的一般回答似乎是RANSAC。 给定模型和一些噪声数据，算法有效地恢复模型的参数 您必须选择一个可以映射数据的简单模型。任何顺利都应该没问题。让我们说几个高斯的混合物。 RANSAC将设置模型的参数并同时估计一组内衬。然后扔掉任何不适合模型的东西。

Answer 8

即使数据不是正态分布，您也可以过滤掉2或3个标准偏差;至少，它将以一致的方式完成，这应该是重要的。

当您删除异常值时，std dev将会更改，您可以循环执行此操作，直到std dev中的更改最小化。是否要执行此操作取决于您为何以这种方式操作数据。一些统计人员对删除异常值有重大保留意见。但是有些人会删除异常值来证明数据是正常分布的。

Answer 9

不是专家，但我的记忆暗示：

• 确定您需要排序和计算的百分位数
• 从数据中获取样本并计算百分位值听起来像是一个好的计划，如果你能得到一个好样本
• 如果不是，正如Henrik建议的那样，如果你做桶并计算它们，你可以避免完全排序

Answer 10

100k元素的一组数据几乎没有时间排序，所以我假设你必须重复这样做。如果数据集只是略微更新的相同集合，那么最好建立一个树（O(N log N)），然后在它们进入时删除并添加新点（O(K log N) K是改变的点数）。否则，已提及的k最大元素解决方案为每个数据集提供O(N)。