查找前10个搜索词的算法
我目前正准备接受采访,这让我想起曾经在之前的一次采访中被问过的一个问题:
“您被要求设计一些软件,以便在Google上连续显示前10个搜索字词。您可以访问一个Feed,该Feed提供目前在Google上搜索的无穷无尽的实时搜索字词流。请说明什么算法您将用于实现此目的的数据结构。您将设计两种变体:
(i)显示所有时间的前10个搜索词(即自您开始阅读Feed以来)。
(ii)仅显示过去一个月的前10个搜索字词,每小时更新一次。
您可以使用近似值获得前10名,但您必须证明自己的选择是合理的。“ 我在这次采访中遭到轰炸,但仍然不知道如何实现这一点。
第一部分要求在无限列表的不断增长的子序列中的10个最频繁的项目。我查看了选择算法,但找不到任何在线版本来解决这个问题。
第二部分使用有限列表,但由于处理的数据量很大,您无法将整个月的搜索项存储在内存中并每小时计算一次直方图。
由于前10名列表不断更新,所以问题变得更加困难,所以你需要在滑动窗口计算前10名。
有什么想法吗?
16 个答案:
答案 0 :(得分:53)
频率估算概述
有一些众所周知的算法可以使用固定数量的存储来为这样的流提供频率估计。一个是Misra和Gries(1982)的 Frequent,。从 n 项目列表中,使用 k - 1 计数器查找超过 n / k 次的所有项目。这是Boyer和Moore的 Majority 算法的一般化(Fischer-Salzberg,1982),其中 k 是2. Manku和Motwani的 LossyCounting (2002) )和Metwally的 SpaceSaving (2005)算法具有相似的空间要求,但可以在某些条件下提供更准确的估计。
要记住的重要一点是,这些算法只能提供频率估算。具体而言,Misra-Gries估计可以通过(n / k)项目来计算实际频率。
假设您有一个算法可以正确识别项目 ,如果它超过50%的时间。为此算法提供 N 个不同项目的流,然后添加另一个 N - 1 一个项目 x 的副本,总计< em> 2N - 1 项目。如果算法告诉您 x 超过总数的50%,则它必须位于第一个流中;如果没有, x 不在初始流中。为了使算法进行此确定,它必须存储初始流(或与其长度成比例的一些摘要)!因此,我们可以向自己证明这种“精确”算法所需的空间为Ω( N )。
相反,这里描述的这些频率算法提供估计,识别超过阈值的任何项目,以及一些低于它的项目。例如,使用单个计数器的 Majority 算法将始终给出结果;如果任何项目超过流的50%,将会找到它。但它也可能会给你一个只出现一次的项目。如果没有对数据进行第二次传递(再次使用单个计数器,但仅查找该项目),您将不会知道。
频繁算法
以下是Misra-Gries的 Frequent 算法的简单描述。 Demaine(2002)和其他人已经对算法进行了优化,但这给了你一个要点。
指定阈值分数, 1 / k ;任何超过 n / k 次的项目都将被找到。创建一个空地图(如红黑树);键将是搜索项,值将是该术语的计数器。
- 查看流中的每个项目。
- 如果地图中存在该字词,请递增关联的计数器。
- 否则,如果地图少于 k - 1 条目,请将该字词添加到地图中,并使用一个计数器。
- 但是,如果地图已经有 k - 1 条目,则减少每个条目中的计数器。如果在此过程中任何计数器达到零,请将其从地图中删除。
请注意,您可以使用固定数量的存储(仅固定大小的地图)处理无限量的数据。所需的存储量仅取决于感兴趣的阈值,并且流的大小无关紧要。
计算搜索次数
在这种情况下,您可能会缓冲一小时的搜索,并对该小时的数据执行此过程。如果您可以在这个小时的搜索日志中进行第二次传递,您可以获得第一次传递中识别出的最高“候选人”的确切发生次数。或者,也许它可以进行一次通过,并报告所有候选人,知道应该包含的任何项目,并且任何额外的只是噪音将在下一个小时消失。
任何真正超出利息门槛的候选人都会被存储为摘要。保留这些摘要一个月的价值,每小时丢掉最旧的摘要,您就可以很好地接近最常见的搜索词。
答案 1 :(得分:46)
嗯,看起来像是一大堆数据,存储所有频率的费用可能过高。 如果数据量太大我们无法将其全部存储起来,我们就会进入数据流算法的域。
该领域的实用书籍: Muthukrishnan - "Data Streams: Algorithms and Applications"
我从上面选择的问题的密切相关参考: Manku, Motwani - "Approximate Frequency Counts over Data Streams" [pdf]
顺便说一句,斯坦福的Motwani(编辑)是非常重要的"Randomized Algorithms"书的作者。 本书第11章讨论了这个问题 。 修改:抱歉,错误的引用,该特定章节是针对不同的问题。检查后,我建议在线提供section 5.1.2 of Muthukrishnan's book。
答案 2 :(得分:19)
这是我目前正在进行的研究项目之一。要求几乎与您的要求完全一致,我们已经开发出很好的算法来解决问题。
输入
输入是无穷无尽的英语单词或短语(我们称之为tokens)。
输出
- 我们已经看到输出前N个代币 远(从我们拥有的所有代币 看到!)
- 在a中输出前N个令牌 历史窗口,比方说,最后一天或 上周。
本研究的应用是在Twitter或Facebook上找到主题的热门话题或趋势。我们有一个爬网程序可以在网站上抓取,它会生成一个单词流,这些单词将输入到系统中。然后,系统将在整体或历史上输出最高频率的单词或短语。想象一下,在过去的几周里,“世界杯”这个词在Twitter上会多次出现。 “保罗章鱼”也是如此。 :)
字符串转换为整数
系统每个单词都有一个整数ID。虽然互联网上几乎有无限可能的单词,但在积累了大量单词之后,找到新单词的可能性变得越来越低。我们已经找到了400万个不同的单词,并为每个单词分配了一个唯一的ID。这整组数据可以作为哈希表加载到内存中,大约消耗300MB内存。 (我们已经实现了自己的哈希表.Java的实现需要巨大的内存开销)
然后可以将每个短语标识为整数数组。
这很重要,因为整数的排序和比较比字符串快。
存档数据
系统会保留每个令牌的归档数据。基本上它是(Token, Frequency)对。但是,存储数据的表会非常庞大,因此我们必须对表进行物理分区。一旦分区方案基于令牌的ngrams。如果令牌是单个单词,则为1gram。如果令牌是双字短语,则为2gram。这继续下去。大概在4克,我们有10亿条记录,桌面大小约为60GB。
处理传入流
系统将吸收传入的句子,直到内存被充分利用(Ya,我们需要一个MemoryManager)。在取N个句子并存储在存储器中之后,系统暂停,并开始将每个句子标记为单词和短语。每个标记(单词或短语)都被计算在内。
对于高频率的令牌,它们总是留在记忆中。对于频率较低的令牌,它们是根据ID排序的(记住我们将String转换为整数数组),并序列化为磁盘文件。
(但是,对于您的问题,由于您只计算单词,因此您可以将所有字频映射仅存储在内存中。精心设计的数据结构将仅消耗300MB内存,用于400万个不同的单词。一些提示:使用用于表示字符串的ASCII字符,这是可以接受的。
同时,一旦找到系统生成的任何磁盘文件,就会激活另一个进程,然后开始合并它。由于磁盘文件已排序,因此合并将采用类似合并排序的类似过程。这里也需要注意一些设计,因为我们希望避免过多的随机磁盘搜索。我们的想法是同时避免读取(合并进程)/写入(系统输出),并在写入不同磁盘时将合并进程从一个磁盘读取。这类似于实现锁定。
结束日期
在一天结束时,系统将有许多频繁的令牌,其频率存储在内存中,而且许多其他频率较低的令牌存储在多个磁盘文件中(并且每个文件都已排序)。
系统将内存映射刷新到磁盘文件中(对其进行排序)。现在,该问题变为合并一组已排序的磁盘文件。使用类似的过程,我们最终会得到一个已排序的磁盘文件。
然后,最后的任务是将已排序的磁盘文件合并到存档数据库中。 取决于存档数据库的大小,如果足够大,算法的工作方式如下:
for each record in sorted disk file
update archive database by increasing frequency
if rowcount == 0 then put the record into a list
end for
for each record in the list of having rowcount == 0
insert into archive database
end for
直觉是,经过一段时间后,插入次数会变得越来越小。越来越多的操作只会进行更新。此更新不会受到索引的惩罚。
希望这整个解释会有所帮助。 :)
答案 3 :(得分:4)
您可以将hash table与binary search tree结合使用。实现一个<search term, count>字典,告诉您每个搜索字词的搜索次数。
显然,每小时迭代整个哈希表以获得前10名非常不好。但这是谷歌,我们正在谈论,所以你可以假设前十名都会得到,比如超过10 000次点击(尽管这可能是一个更大的数字)。因此,每当搜索项的计数超过10 000时,请将其插入BST。然后每小时,您只需要从BST获得前10个,其中应包含相对较少的条目。
这解决了历史最高的10个问题。
真正棘手的部分是处理一个术语在月度报告中占据另一个位置(例如,“堆栈溢出”在过去两个月可能有5万次点击,但过去一个月只有10 000次,而“亚马逊”过去两个月可能有40 000个,但过去一个月可能有3万个。你希望“amazon”在你的月度报告中出现“堆栈溢出”之前。要做到这一点,我会为所有主要(超过10 000个所有时间搜索)搜索条件存储一个30天的列表,该列表告诉您每天搜索该术语的次数。该列表将像FIFO队列一样工作:您删除第一天并每天插入一个新的(或每小时,但随后您可能需要存储更多信息,这意味着更多的内存/空间。如果内存不是问题,请执行此操作它,否则去他们所说的“近似”)。
这看起来是一个好的开始。然后,您可以担心修剪具有&gt;的条款。 10 000次点击,但很长一段时间没有很多这样的东西。
答案 4 :(得分:3)
案例i)
维护所有搜索项的哈希表,以及与哈希表分开的排序前十名列表。每当发生搜索时,递增哈希表中的相应项目,并检查现在是否应该使用前十名列表中的第10项切换该项目。
O(1)查找前十个列表,并将max O(log(n))插入哈希表(假设冲突由自平衡二叉树管理)。
案例ii) 我们维护一个哈希表和所有项的排序列表,而不是维护一个巨大的哈希表和一个小列表。每当进行搜索时,该术语在哈希表中递增,并且在排序列表中,可以检查该术语以查看它是否应该在其之后切换。自平衡二叉树可以很好地工作,因为我们还需要能够快速查询它(稍后将详细介绍)。
此外,我们还以FIFO列表(队列)的形式维护一个“小时”列表。每个'小时'元素将包含在该特定小时内完成的所有搜索的列表。例如,我们的小时列表可能如下所示:
Time: 0 hours
-Search Terms:
-free stuff: 56
-funny pics: 321
-stackoverflow: 1234
Time: 1 hour
-Search Terms:
-ebay: 12
-funny pics: 1
-stackoverflow: 522
-BP sucks: 92
然后,每小时:如果列表长度至少为720小时(即30天内的小时数),请查看列表中的第一个元素,对于每个搜索词,减少哈希表中的元素适当的金额。然后,从列表中删除第一小时元素。
所以我们说我们是在721时,我们已准备好查看列表中的第一个小时(上图)。我们在散列表中减少56个免费的东西,用321等减少有趣的图片,然后将完全从列表中删除0小时,因为我们永远不需要再次查看它。
我们维护一个允许快速查询的所有术语的排序列表的原因是因为我们在720小时前完成搜索术语后的每个小时,我们需要确保前十个列表保持排序。因此,当我们在哈希表中减少56的“免费东西”时,我们会检查它现在在列表中的位置。因为它是一个自平衡的二叉树,所以这一切都可以在O(log(n))时间内很好地完成。
编辑:牺牲空间的准确性......
在第一个中实现一个大列表可能很有用,就像在第二个中一样。然后我们可以在两种情况下应用以下空间优化:运行cron作业以删除列表中除顶部 x 项之外的所有项目。这将降低空间要求(因此可以更快地在列表上进行查询)。当然,它会产生近似结果,但这是允许的。可以在根据可用内存部署应用程序之前计算 x ,并在有更多内存可用时动态调整。
答案 5 :(得分:2)
粗略思考......
前10名
- 使用哈希集合,其中存储每个术语的计数(清理术语等)
- 一个排序的数组,其中包含正在进行的前10位,只要术语的计数等于或大于数组中的最小计数,就会添加到此数组中的术语/计数
每月更新每月排名前10位:
- 使用从开始模744(一个月内的小时数)开始经过的小时数索引的数组,哪些数组条目包含哈希集合,其中存储了在此小时槽期间遇到的每个术语的计数。只要小时槽计数器发生变化,就会重置一个条目
- 每当当前小时槽计数器发生变化(最多每小时一次)时,需要收集在小时槽上编入索引的数组中的统计数据,方法是复制并展平在小时槽上索引的此数组的内容
错误......有意义吗?我并没有像在现实生活中那样思考这个问题
啊是的,忘记提及,每月统计数据所需的每小时“复制/展平”实际上可以重复使用前10个相同的代码,这是一个很好的副作用。
答案 6 :(得分:2)
精确解决方案
首先,这个解决方案可以保证正确的结果,但需要大量的内存(大图)。
“所有时间”变种
维护一个哈希映射,将查询作为键,将其计数作为值。此外,保留目前为止最常见的10个查询列表以及第10个最常见计数(阈值)的计数。
在读取查询流时不断更新地图。每次计数超过当前阈值时,请执行以下操作:从“前10名”列表中删除第10个查询,将其替换为刚刚更新的查询,并同时更新阈值。
“过去一个月”变种
保持相同的“前10名”列表并以与上述相同的方式更新。此外,保留一个类似的地图,但这次存储30 * 24 = 720计数(每小时一个)的矢量作为值。每小时对每个键执行以下操作:从向量中删除最旧的计数器,在末尾添加一个新的计数器(初始化为0)。如果向量为全零,则从地图中删除密钥。此外,您每小时都必须从头开始计算“前10名”。
注意:是的,这次我们存储了720个整数而不是一个,但是密钥要少得多(所有变量都有真正的长尾)。
逼近
这些近似值并不能保证正确的解决方案,但耗费的内存更少。
- 处理每个第N个查询,跳过其余查询。
- (仅适用于所有时间变体)保留地图中最多M个键值对(M应该尽可能大)。它是一种LRU缓存:每次读取不在地图中的查询时,删除最近最少使用的查询,并将其替换为当前处理的查询。
答案 7 :(得分:2)
过去一个月的前10个搜索字词
使用内存有效的索引/数据结构,例如tightly packed tries(来自tries上的维基百科条目)近似定义了内存需求与n个术语之间的某种关系。
如果所需内存可用(假设1 ),您可以保留确切的每月统计信息,并将其每月汇总到所有时间统计信息中。
此处还有一个假设,即将“上个月”解释为固定窗口。 但即使每月窗口滑动,上面的过程也显示了原理(滑动可以用给定大小的固定窗口近似)。
这让我想起round-robin database,除了一些统计数据是在“所有时间”计算的(在某种意义上并非所有数据都被保留; rrd通过平均,总结或选择最大值来合并时间段而忽略细节/ min值,在给定的任务中,丢失的细节是关于低频项目的信息,这可能会引入错误。)
假设1
如果我们不能保持整个月的完美统计数据,那么我们应该能够找到一个特定的时期P,我们应该能够保持完美的统计数据。
例如,假设我们在某个时间段P上有完美的统计数据,这个时间段为n个月
完美统计定义函数f(search_term) -> search_term_occurance。
如果我们可以将所有n完美统计表保存在内存中,那么可以按以下方式计算每月统计数据的滑动:
- 添加最新时段的统计信息
- 删除最早期间的统计信息(因此我们必须保留
n完美的统计信息表)
但是,如果我们只在汇总级别(每月)保留前十名,那么我们将能够从固定期间的完整统计数据中丢弃大量数据。这给出了一个已经固定的工作程序(假设时间段P的完美统计表的上限)内存要求。
上述程序的问题在于,如果我们仅为滑动窗口保留信息(同样适用于所有时间),那么统计数据对于在一段时间内达到峰值的搜索项来说是正确的,但可能没有看到随着时间的推移不断渗透的搜索词的统计数据。
这可以通过保留超过前10个术语的信息来抵消,例如前100个术语,希望前10名是正确的。
我认为进一步的分析可能会将条目所需的最小出现次数与统计数据的一部分联系起来(与最大错误有关)。
(在决定哪些条目应成为统计数据的一部分时,还可以监视和跟踪趋势;例如,如果每个术语的每个时期P中出现的线性推断告诉您该术语将在一个月内变得重要或者您可能已经开始跟踪它。类似的原则适用于从跟踪池中删除搜索词。)
对于上述情况,最糟糕的情况是当你有很多几乎同等频繁的术语并且它们一直在变化时(例如,如果仅跟踪100个术语,那么如果前150个术语同样频繁出现,但前50个术语更频繁地出现在第一个月,以免经常一段时间后,统计数据将无法正确保存。
此外,可能还有另一种方法在内存大小上没有固定(严格来说也不是上述方法),这将根据事件/周期(日,月,年,所有时间)定义最小重要性。保持统计数据。这可以保证聚合期间每个统计数据的最大误差(再次参见循环)。
答案 8 :(得分:2)
"clock page replacement algorithm"(也称为“第二次机会”)的改编怎么样?如果搜索请求均匀分布,我可以想象它能够很好地工作(这意味着大多数搜索的术语会定期出现,而不是连续出现5次,然后再也不会出现。)
以下是算法的直观表示: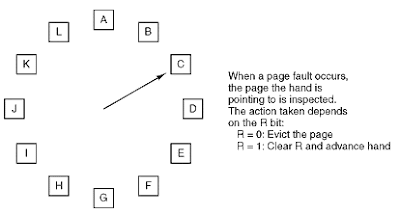
答案 9 :(得分:0)
将搜索项的计数存储在巨型哈希表中,其中每个新搜索都会使特定元素增加1。跟踪前20个左右的搜索字词;当第11位的元素递增时,检查是否需要用#10 *交换位置(没有必要保持前10个排序;你关心的只是区分10和11)。
* 需要进行类似的检查以查看新的搜索词是否位于第11位,因此该算法也会向下扩展到其他搜索词 - 所以我简化了一点。 < / p>
答案 10 :(得分:0)
有时最好的答案是“我不知道”。
我会更深入地刺痛。我的第一直觉是将结果提供给Q.一个过程将不断处理进入Q的项目。该过程将保留一张地图
术语 - &gt;计数
每次处理Q项时,您只需查找搜索项并增加计数。
与此同时,我会维护一份对地图中前10个条目的引用列表。
对于当前实现的条目,查看其计数是否大于前10个中最小条目的计数。(如果不在列表中)。如果是,请用条目替换最小的。
我认为这样可行。没有时间密集的操作。您必须找到一种方法来管理计数图的大小。但这对于面试答案应该足够好了。
他们不期待一个解决方案,想看看你是否能够思考。你不必在那里写出解决方案......
答案 11 :(得分:0)
一种方法是,对于每次搜索,您都存储该搜索词及其时间戳。这样,在任何时间段内找到前十名只是在给定时间段内比较所有搜索词。
算法很简单,但缺点是内存和时间消耗更大。
答案 12 :(得分:0)
如何使用包含10个节点的Splay Tree?每次尝试访问树中未包含的值(搜索项)时,抛出任何叶子,插入值并访问它。
这背后的想法与我的其他answer相同。假设搜索条件均匀/定期访问,此解决方案应该能够很好地运行。
修改
还可以在树中存储更多搜索词(我在其他答案中建议的解决方案也是如此),以便不删除可能很快再次访问的节点。一个人存储的值越多,结果就越好。
答案 13 :(得分:0)
但是,如何计算特定搜索的频率将计入其他内容。 也许正如大家所说,数据流算法......
答案 14 :(得分:0)
使用cm-sketch存储自开始以来所有搜索的计数,保留最小10的最小堆。 对于每月结果,保持30厘米草图/哈希表和最小堆,每个开始计数和更新从最后30,29 ..,1天。作为日间通行证,清除最后一个并将其用作第1天。 对于每小时结果相同,保持60个哈希表和最小堆并开始计算最后60,59,... 1分钟。作为一分钟通过,清除最后一个并将其用作分钟1。
Montly结果在1天的范围内是准确的,每小时结果在1分钟的范围内是准确的
答案 15 :(得分:0)
当你有一个固定数量的内存和一个'无限'(想象非常大)的令牌流时,这个问题不是普遍可以解决的。
粗略解释......
要了解原因,请考虑输入流中每N个令牌都有一个特定令牌(即单词)T的令牌流。
此外,假设内存可以将引用(字ID和计数)保存到最多M个令牌。
根据这些条件,可以构造一个输入流,如果N足够大,将永远不会检测到令牌T,以便流在T之间包含不同的M个令牌。
这与前N个算法细节无关。它只取决于M的限制。
要了解为什么这是真的,请考虑由两个相同令牌组成的传入流:
T a1 a2 a3 ... a-M T b1 b2 b3 ... b-M ...
其中a和b都是不等于T的有效令牌。
请注意,在此流中,每个a-i和b-i的T出现两次。然而,似乎很少能从系统中冲洗出来。
从空内存开始,第一个令牌(T)将占用内存中的一个插槽(以M为界)。然后a1将消耗一个槽,当M耗尽时,一直到a-(M-1)。
当a-M到达时,算法必须丢弃一个符号,所以让它成为T. 下一个符号将是b-1,这将导致a-1被刷新等等。
因此,T不会保留足够长的内存驻留时间以构建实数。简而言之,任何算法都会错过具有足够低的本地频率但高全局频率(在流的长度上)的令牌。
- 我写了这段代码,但我无法理解我的错误
- 我无法从一个代码实例的列表中删除 None 值,但我可以在另一个实例中。为什么它适用于一个细分市场而不适用于另一个细分市场?
- 是否有可能使 loadstring 不可能等于打印?卢阿
- java中的random.expovariate()
- Appscript 通过会议在 Google 日历中发送电子邮件和创建活动
- 为什么我的 Onclick 箭头功能在 React 中不起作用?
- 在此代码中是否有使用“this”的替代方法?
- 在 SQL Server 和 PostgreSQL 上查询,我如何从第一个表获得第二个表的可视化
- 每千个数字得到
- 更新了城市边界 KML 文件的来源?