弹道曲线问题

Question

好的我知道这对于程序员来说是非常偏离主题的，但我仍然需要这个应用程序，所以这里是：

弹道曲线（没有风或任何其他条件）由这两行指定：

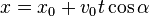
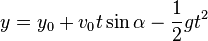
因此，存在一个问题，即您有3个未知值：x，y和时间t，但只有2个方程式。 你不能用这些值真正计算所有3，我得到了：

• velocity v
• angle Alpha
• 原点坐标

因此，您必须决定指定哪一个。

现在你有2D坦克游戏，或类似的东西，你知道你有坦克和使用弹道，你必须用设定的角度和力量射击对手。

我需要知道当子弹击中地面时，它可以在飞行时进行播出或预先计算。 出现了我的问题。哪种方式使用？在每个步骤中预先计算或检查击中地面。

如果我想预先计算，我需要知道地形的高度，这在逻辑上必须是恒定的，因为我不知道在哪个x坐标。如果我知道X，那就意味着我的炮塔前面就是墙。因此，当我到达地面时，唯一可以获得结果的方法是检查击中地面的时间间隔。这也很好，因为地形没有顶部静态yay！但这不是太大的开销，可以变得更简单吗？你遇到过这样的问题/解决方案吗？

在此先感谢，顺便说一句，地形可以是平坦的，使用线条或NURBS，所以我请求一般的解决方案，而不是特定的，因为你拍摄的高度会影响。

Answer 1

您可以通过求解y(x)的一个等式并替换为另一个等式来计算射弹t的路径。你得到了

然后找到着陆点是计算该函数与定义地形高度的函数之间的交点。一个交叉点将是发射点，另一个交叉点将是着陆点。 （如果你的地形非常陡峭且多山，那么可能会有两个以上的交叉点，在这种情况下，你会选择第一个交叉点，x大于启动点。）你可以使用各种root-finding algorithms实际计算交叉点;检查您必须查看的数学或游戏物理库的文档是否提供了执行此操作的方法。

Answer 2

David Zaslavsky很好地回答了关于求解方程式的问题，但如果你的最终目标是简单的弹道学模拟，我建议你使用向量分解。

通过利用矢量分解，您可以推导出射弹的x和y能力矢量。然后，您可以对每个组件应用加速度以考虑重力，风等。然后您可以将每个间隔的射弹（x，y）位置更新为时间的函数。

例如：

double Speed = 100.0;     // Speed rather than velocity, as it is only the magnitude
double Angle = 30.0;      // Initial angle of 30º
doulbe Position[2] = {0.0,0.0};  // Set the origin to (0,0)

double xvelocity = Speed * Cos(Angle);
double yvelocity = Speed * Sin(Angle);

然后，如果您可以按如下方式实现简单的更新功能：

void Update(double Time)
{
     yvelocity = -9.8 * Time; // Apply gravity

     Position[0] *= (xvelocity * Time);  // update x position
     Position[1] *= (yvelocity * time);  // update y position

     CheckCollisions();  // check for collisions
}

当然这是一个非常的基本示例，但您可以从此处构建它。

Answer 3

幸运的是，这是非常简单的运动学。

这些方程式是参数化的：对于任何给定时间t，它们会为您提供该时间的x和y坐标。您需要做的就是插入起始速度v和角度a。

如果你在平地上工作，你的射弹降回的时间就是2sin（a）v / g，即你的速度的垂直分量除以重力引起的向下加速度。 2是因为速度降低到0需要花费这么多时间，然后再次加速回落。一旦你知道了解决x的时间。

如果你的地形不平坦，你还有一些额外的乐趣。你可以试试的是找出在相同高度撞击地面的时间，然后校正额外的垂直距离。这也会改变你的水平距离，这可能会再次影响你的身高...但是两次或三次调整，误差太小，人类无法注意到：）

Answer 4

我不确定你是否正确这样做。你想要的主要方程是s = si + vi*dt + .5*adtdt。这是一个简单的一维方程，但它可以干净地推广到向量。

实际上，si是你的初始位置，vi是你的初始速度，a是由重力引起的加速度。

为了完成这项工作，建立一个完美的水平初速度矢量，并将其投射到发射角度。那是你的vi。 Si将是枪管的尖端。从那里它是矢量求和和缩放。

Answer 5

连续功能对计算机不起作用，因为计算机是隐式离散的：浮动/双数是离散的，计时器是离散的，游戏网格是离散的（即使它使用'双打'）。

所以，就像Justin Holdsclaw所建议的那样，对方程式进行离散化。在每个方向都有速度和加速度矢量（在你的情况下是X和Y;你也可以添加Z）。在每个刻度处更新所有向量和对象在空间中的位置。

请注意，结果不会是“完全”。 “delta”值（网格粗糙度）越小，越接近“精确”曲线。要准确了解有多接近 - 如果您有兴趣，可以找一本关于数值分析的书，并阅读前几章。出于实用目的，您可以尝试一下。