Haskell中的数字说明

Question

我希望明确解释Num，Real，Integral，Integer，Int，Ratio，{{1} }，Rational，Double。

Answer 1

这个答案主要假设你知道类型和类型类之间的区别。如果这个差异对你来说是朦胧的，那么在阅读之前就会clear up your understanding。

<强>货号

Num是一个包含所有数字类型的类型类。

:info Num
class Num a where
  (+) :: a -> a -> a
  (-) :: a -> a -> a
  (*) :: a -> a -> a
  negate :: a -> a
  abs :: a -> a
  signum :: a -> a
  fromInteger :: Integer -> a
        -- Defined in ‘GHC.Num’
instance Num Word -- Defined in ‘GHC.Num’
instance Num Integer -- Defined in ‘GHC.Num’
instance Num Int -- Defined in ‘GHC.Num’
instance Num Float -- Defined in ‘GHC.Float’
instance Num Double -- Defined in ‘GHC.Float’

<强>实时

还有一个类型类，涵盖那些可以表示为实数值的类型（Rational类型）。

:info Real
class (Num a, Ord a) => Real a where
  toRational :: a -> Rational
        -- Defined in ‘GHC.Real’
instance Real Word -- Defined in ‘GHC.Real’
instance Real Integer -- Defined in ‘GHC.Real’
instance Real Int -- Defined in ‘GHC.Real’
instance Real Float -- Defined in ‘GHC.Float’
instance Real Double -- Defined in ‘GHC.Float’

<强>积分

积分的类型类，您知道...,-2,-1,0,1,...。诸如Integer（aka big int），Int，Int64等类型是实例。

:info Integral
class (Real a, Enum a) => Integral a where
  quot :: a -> a -> a
  rem :: a -> a -> a
  div :: a -> a -> a
  mod :: a -> a -> a
  quotRem :: a -> a -> (a, a)
  divMod :: a -> a -> (a, a)
  toInteger :: a -> Integer
        -- Defined in ‘GHC.Real’
instance Integral Word -- Defined in ‘GHC.Real’
instance Integral Integer -- Defined in ‘GHC.Real’
instance Integral Int -- Defined in ‘GHC.Real’

<强>整数

类型，而不是类型类，例如我们到目前为止所讨论的类型，它可以表示无界整数。所以2^3028是合法的价值。

<强>内部

固定宽度积分。在GHC编译器中，这是32位或64位，具体取决于您的体系结构。 Haskell语言只保证至少29位。

<强>比率

这是一个类型构造函数，因此您可以说Ratio Integer之类的内容来获取两个整数的比率类型（数学a/b）。

<强>理性

理性确实是两个整数的比率，理解比率并且你很好：

:i Rational
type Rational = Ratio Integer

<强>双

双精度浮点值的类型。

<强>浮

单精度浮点值的类型。

Answer 2

Haskell documentation中有一个有趣的图像，显​​示了类及其类型实例之间的关系，涵盖了你提到的大部分内容：

关于Rational numbers：

  

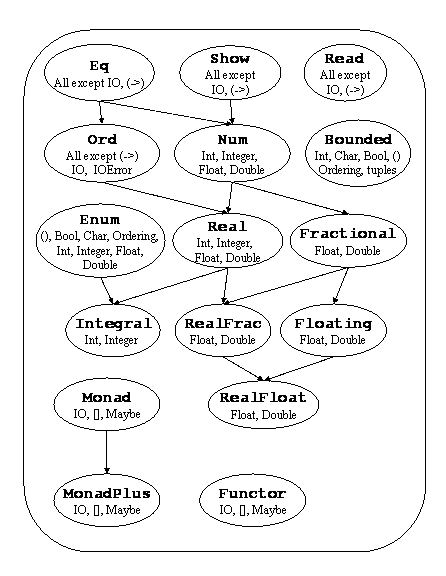
对于每个Integral类型t，有一个理性对Ratio类型   使用类型为t的组件。类型名称Rational是其同义词   Ratio Integer。