Question

据我所知，大多数递归函数都可以使用循环重写。有些可能比其他人更难，但大多数都可以重写。

在哪些情况下，使用循环重写递归函数是不可能的（如果存在这样的条件）？

Answer 1

当您递归使用函数时，编译器会为您处理堆栈管理，这使得递归成为可能。你可以递归地执行任何操作，你可以通过自己管理堆栈来做（对于间接递归，你只需要确保你的不同函数共享该堆栈）。

所以，不，没有什么可以通过递归完成，并且无法通过循环和堆栈来完成。

Answer 2

任何递归函数都可以迭代（循环）但你需要自己使用堆栈来保持状态。

通常，尾递归很容易转换为循环：

A(x) {
  if x<0 return 0;
  return something(x) + A(x-1)
}

可以翻译成：

A(x) {
  temp = 0;
  for i in 0..x {
    temp = temp + something(i);
  }
  return temp;
}

其他可以转换为尾递归的递归也很容易改变。另一个需要更多的工作。

以下内容：

treeSum(tree) {
  if tree=nil then 0
  else tree.value + treeSum(tree.left) + treeSum(tree.right);
}

翻译不是那么容易。你可以删除一个递归，但如果没有一个结构来保持状态，那么另一个递归是不可能的。

treeSum(tree) {
  walk = tree;
  temp = 0;
  while walk != nil {
    temp = temp + walk.value + treeSum(walk.right);
    walk = walk.left;
  }
}

Answer 3

每个递归函数都可以通过一个循环实现。

只要想想处理器的作用，它就会在一个循环中执行指令。

Answer 4

我不知道递归函数无法转换为迭代版本的示例，但不切实际或效率极低的示例是：

基本上，你必须开始跟踪无限的潜在状态。

Answer 5

并不是因为它们无法使用循环实现，事实上递归算法的工作方式，它更清晰，更简洁（在许多情况下在数学上可证明）函数是正确的

许多递归函数可以写成尾循环递归，可以优化为循环，但这取决于算法和使用的语言。

Answer 6

它们都可以写成迭代循环（但有些可能仍然需要一个堆栈来保留以前的状态以便以后的迭代）。

Answer 7

从递归转换到迭代非常困难的一个例子是Ackermann function。

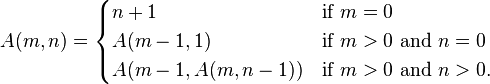
$alt text$

Answer 8

间接递归仍然可以转换为非递归循环;从其中一个函数开始，并内联对其他函数的调用，直到你有一个直接递归函数，然后可以将其转换为使用堆栈结构的循环。

Answer 9

在SICP中，作者要求读者提出一种纯粹的迭代方法来实现“计数变化”问题（来自Project Euler的here's an example）。

但是已经给出了对你的问题的严格答案 - 循环和堆栈可以实现任何递归。

Answer 10

您始终可以使用循环，但您可能需要创建更多数据结构（例如，模拟堆栈）。